2022-07-09 • cryo-EM

标签页 Tags： cryo-EM

本站自2019年7月已访问 web counter

傅里叶与图像的关系

离散二维傅里叶变换
傅里叶变换的特征
卷积与卷积定理
- 卷积
- 卷积定理
傅里叶域分辨率
- 低通（Low-Pass）与高通（High-Pass）过滤
相关系数函数

参考自 Jachim Frank 著作的《Three-Dimensional Electron Microscopy of Macromolecular Assemblies》

离散二维傅里叶变换

元素图像（elementary images）的数学表征

假设一个矩形的图像，我们把他的长和宽分别分别分割为 $K$ 与 $I$ 份，分割后的每一小部分分别用 $\Delta y$ 与 $\Delta x$ 表示，这样就可以通过这四个符号表示该矩形图像的长和宽，如下图所表示

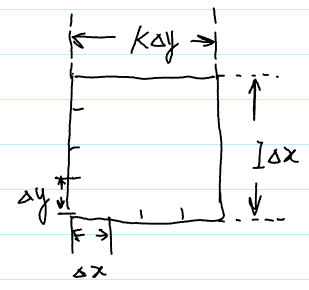
则电镜所得分子在二维方向上的投影表示为，

$$ p_{ik} = p(x_{i}, y_{k}); i = 1,…,I; k = 1,…,K\tag{1} $$

傅里叶如何表征图像特征

傅里叶变换利用正弦曲线或者复指数形式作为基函数（基函数）去表征图像信息。作为可以表征图像中包含信息的另一种方法，从正交归一化基函数集合的许多其他扩展中选择傅里叶变换的原因如下：

容易地分析仪器相差的影响以及对象中周期性的存在。
提供了理解投影和它们所源自的对象之间的关系。
理解三维重建原理的关键。

使用傅里叶去表征图像以一系列基图像（elementary images）集合作为基函数。

以正弦变换为例，这时这些基图像为正弦密度分布：

$$ e_{lm|_{ik}} = e_{lm}(x_{i}, y_{k})=\sin[2\pi(u_{l}x_{i} + v_{m}y_{k})] \tag{2} $$

我们给出两个新的参数来描述周期性质，如下

$$ \begin{cases} u_{l} = \frac{l}{I\Delta x}, & l=0, … , I-1 \\ \\ v_{m} = \frac{m}{k\Delta y}, & m=0, … , K-1 \end{cases}\tag{3} $$

每个图像由正方形晶格位置（ $x_{i}$, $y_{k}$ ）处的离散像素集表示，其特征在于离散傅里叶空间频率分量（ $u_{l}$, $v_{m}$ ）描述在水平（ $l$ ）和垂直方向（ $m$ ）适合框架中的全波数量。见下图

其中可见 $l$ 和 $m$ 可以控制基图像的方向。

使用适当的振幅 $a_{lm}$ 与波相位 $\varphi_{lm}$，任何离散图像 ${p_{ik}; i=1,…,I; k=1,…,K}$ 可以用基图像的叠加来表示，

$$ p_{ik} = p(x_{i}, y_{k})= \sum_{l=0}^{I-1}\sum_{m=0}^{K-1}a_{lm}\sin{\left[2\pi\left(\frac{li}{I} + \frac{mk}{K}\right) + \phi_{lm}\right]}\tag{4} $$

其中，

$$ \begin{cases} u_{l} = l/(I\Delta x) \\ v_{m} = l/(K\Delta y) \\ x = i\Delta x \\ y = k\Delta y \\ \end{cases} $$

傅里叶表征图像的常用表达式

实际中，傅里叶表示的方法与 $eqn(3)$ 往往不同，常利用“圆形”复指数波：

$$ \exp\left[-2\pi i\left(\frac{li}{I} + \frac{mk}{K}\right)\right]=\cos\left[2\pi\left(\frac{li}{I} + \frac{mk}{K}\right)\right] + i\sin\left[2\pi\left(\frac{li}{I} + \frac{mk}{K}\right)\right]\tag{5} $$

以便更容易处理数学公式。

傅里叶公式去表征一个图象的方法如下，

$$ p_{ik} = \sum_{l=0}^{I-1}\sum_{m=0}^{K-1}F_{lm}\exp{\left[-2\pi i\left(\frac{li}{I}+\frac{mk}{K}\right)\right]}\tag{6} $$

用符号表示为，

$$ p(x, y) = \mathfrak{F}\lbrace F(u, v)\rbrace , \phantom{kkk} \text{(“Fourier synthesis”)} \tag{7} $$

相反地，给定图像，也可以通过类似的互逆表达式获得傅里叶系数 $F_{lm}$：

$$ F_{lm} = \sum_{l=0}^{I-1}\sum_{m=0}^{K-1}p_{ik}\exp{\left[2\pi i\left(\frac{li}{I} + \frac{mk}{K}\right)\right]}\tag{8} $$

符号表达式为，

$$ F(u,v)=\mathfrak{F}^{-1}\lbrace p(x,y)\rbrace, \phantom{kkk} \text{(“inverse Fourier transformation”)} \tag{9} $$

傅里叶变换的特征

线性（Linearity）特征

如果一幅图像为两张图像的线性结合，

$$ f(\mathbf{r}) = c_{1}f_{1}(\mathbf{r}) + c_{2}f_{2}(\mathbf{r}) $$

则其傅里叶变换为，

$$ \begin{cases} F(\mathbf{k}) = c_{1}F_{1}(\mathbf{k}) + c_{2}F_{2}(\mathbf{k}) \\ \\ F(\mathbf{k}) = \mathfrak{F}\lbrace f(\mathbf{r})\rbrace \end{cases}\tag{10} $$

参数缩放特征

同一物体在不同放大倍数下的不同图像，

$$ f_{2}(\mathbf{r}) = f_{1}(s\mathbf{r}) $$

其中 $s$ 为比例因子，其傅里叶变换为，

$$ \begin{cases} F_{2}(\mathbf{k}) = F_{1}(1/s \mathbf{k}) \\ \\ F(k) = \mathfrak{F}\lbrace f(\mathbf{r})\rbrace \end{cases}\tag{11} $$

对称性质

通过 $eqn(8)$ 可以看到，对于实值函数正常复值傅里叶变换具有以下性质：

$$ F_{-l-m} = [F_{lm}]^{\ast}\tag{12} $$

在 X 射线晶体学中，该式被成为弗里德尔对称（Friedel sysmmetry），

其中星号代表取复共轭，即：

$$ [F_{lm}]^{\ast} = \lbrace \mathfrak{R}\mathrm{e}\lbrace F_{lm}\rbrace, -\mathfrak{I}\mathrm{m}\lbrace F_{lm}\rbrace\rbrace \tag{13} $$

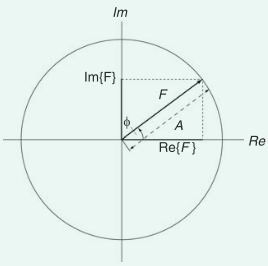
可将复数 $F$ 表示为复平面中的向量。其中 $A$ 为振幅或者模（modulus），表示向量的长，而 $\phi$ 为相位，表示为角（逆时针 counterclockwise 为正）表示向量相对于实轴的旋转。

由傅里叶的对称性质，对于实值图像，傅里叶变换的一半确定另一半的值，所以在所有计算和存储中通常只需要一半。

振幅和相位

复系数 $F_{lm}$ 可以通过复平面中的一个向量来表示，如上图所示。

其长度（傅里叶变换的振幅）为，

$$ |F_{lm}| = [|\mathfrak{R}\mathrm{e}\lbrace F_{lm}\rbrace|^2 + |\mathfrak{I}\mathrm{m}\lbrace F_{lm}\rbrace |^{2}]^{1/2}\tag{14} $$

其相位为，

$$ \varphi_{lm} = \arctan[\mathfrak{I}\mathrm{m}\lbrace F_{lm}\rbrace /\mathfrak{R}\mathrm{e}\lbrace F_{lm}\rbrace]\tag{15} $$

移位定理

当图像按照向量 $\Delta\mathbf{r}= (\Delta x, \Delta y)$ 平移，得到图像 $p(x+\Delta x, y+\Delta y)$ ，其傅里叶变换根据 $eqn(8)$ 与指数因子相乘，有

$$ \mathfrak{F}^{-1}\lbrace p(x+\Delta x, y + \Delta y)\rbrace =F(u, v)\exp[2\pi i(u\Delta x+ v\Delta y)]\tag{16} $$

卷积与卷积定理

卷积

假设我们能够在 $(x_{i}, y_{k})$ 处，形成物体的单点图像。由于分辨率限制，该单点将会在图像平面相关点 $(x_{i}, y_{k})$ 处形成一个圆盘形状。在明场电子显微镜中，应用对于生物大分子成像更加好的弱相位物体（ wweak phase objects ）估计方法，成像可以通过线性叠加的方式构成：两个物点的图像可以通过将两个点独立且分别成像所获得的图像相加来获得。除此以外，EM中还有一个更具限制性的特性，即等平面特性：点的图像看起来是相同的，无论其在图像场中的位置如何。

由以上条件，物体与所成像之间的关联可以由以下给出，

$$ p(x_{i}, y_{k}) = \sum_{l=1}^{I}\sum_{m=1}^{K}o(x_{i},y_{k})h(x_{l}-x_{i}, y_{m}-y_{k}) \tag{17} $$

其中，$i$，$k$，$l$，$m$ 为规则采样网格的相关位置，而 $h(x,y)$ 为点扩散函数（ point-spread function ）—— 即放置在（0,0）处的单个对象点的图像。 $eqn(17)$ 中所描述的关系来自于线性叠加以及等平面特性，其描述了 $o(x,y)$ 与 $h(x,y)$ 之间的卷积。我们将利用符号表示为，

$$ o(x,y)\circ h(x,y) $$

$\delta$ 函数是一种由单点组成的特殊点扩散函数，

$$ h(x_{l}-x_{i}, y_{m}-y_{k}) = \delta(x_{l}-x_{i}, y_{m}-y_{k}) $$

其在 $x_{l} = x_{i}$，$y_{m}=y_{k}$ 时取值为 1, 其他时为 0，

$$ \begin{cases} 1 && x_{l}=x_{i}, y_{m}=y_{k} \\ \\ 0 && \text{其他情况} \end{cases} $$

由 $eqn(17)$ 可得，

$$ p(x_{i}, y_{k}) = o(x_{i},y_{k}) $$

即与 $\delta$ 函数的卷积再现原函数。

卷积定理

卷积定理对于卷积表达式的计算非常重要。即为两函数卷积的傅里叶变换等价于他们自身乘积的傅里叶变换。

由此引申计算 $o(x,y)\circ h(x,y)$：

计算 $H(u,v)=\mathfrak{F}\lbrace h(x,y)\rbrace$
计算 $O(u,v)=\mathfrak{F}\lbrace o(x,y)\rbrace$
计算傅立叶变换后的两函数乘积

$$ P(u,v)=O(u,v)\cdot H(u,v)\tag{18} $$

后可通过计算反向傅里叶变换求出代求结果：

$$ p(s,y)=\mathfrak{F}^{-1}\lbrace P(u,v)\rbrace\tag{19} $$

因为快速傅里叶变换算法的出现（FFT），该步骤要比线性叠加求和的直接结算更有效。

傅里叶域分辨率

采用傅里叶展示图片是存在实际限制的。无论是正弦波亦或复指数表示，比图像中最小特征的尺寸小的波长是不携带任何信息的。

这种信息限制可以用空间频率半径来表示，

$$ R=\sqrt{u^2+v^2} $$

超过某一半径下，如 $R = R_{0}$，超出了傅里叶平面中的大致圆形区域之外，这时将会失去有意义的傅里叶组分。这一边界被称为 bondlimit 或者分辨率限制（空间频率单位，维度为1/长度）。

根据卷积定理，图像中的任何这种扩散或模糊都通过物体的傅里叶变换与在空间频率域中具有有限半径的函数相乘来表示。

低通（Low-Pass）与高通（High-Pass）过滤

对于我们专门处理的非晶体物体，傅里叶变换的信号和噪声分量是叠加的，通常是不可分的。然而，作为空间频率半径 $R$ 的函数，这两个分量经常具有不同的行为：当信号分量在分辨率极限处下降时，噪声分量在该极限之外具有显著的贡献。因此，这样的图像的傅立叶变换与截止（cut-off）函数的相乘：

$$ L(u,v) = \begin{cases} 1 &&& R = \sqrt{u^2 + v^2} = R_{0} \\ \\ 0 &&& \text{其他情况} \end{cases}\tag{20} $$

这样将会根除信号组分，并增强信噪比。这种函数或其变体具有平滑的过渡，而不会呈现尖锐的截断现象（cut-off），被称作低通滤波（low-pass filtration），因为其仅能允许通过低空间频率的傅里叶组分。

具有平滑径向过滤的函数通常是首选的滤波方式，因为 $eqn(20)$ 的滤波方式将会导致图像特征的认为增强，其大小对应于截止处的空间频率。用于傅里叶滤波的最“温和”函数是具有高斯轮廓的函数。

$$ L(u,v)=\exp{[-(u^2+v^2)/R_{0}^2]} $$

其衰减行为由参数 $R_{0}$ 控制：在空间频率半径 $R=\sqrt{u^2+v^2}=R_{0}$ 处，滤波函数将傅里叶振幅减小到其原始值的 $1/e$ 。

曲曲的秘密学术基地