前言
到了 1960 年左右,也就是目前的像差校正电子显微镜时代之前,电子不稳定性已经被降低到了影响 TEM 相差的程度,包括三阶球面像差( $C_{s}$ ),色差( chromatic aberration, $C_{c}$ )。很多论文中讨论了在射线方程的推导中出现高阶项的后果。由于包含这些术语而导致的偏离完美成像的部分,按照光学中对应的像差进行类比分类。保留 $r^3$ 中的项,类似于将 $\theta^3$ 中的项包含在适用于玻璃透镜的 Snell’s 定律中使用的 $\sin\theta$ 的展开中。结果是产生了三阶像差,其中球面像差在高分辨率下最为重要。
大多数高分辨率图像以高放大倍率( $M\gt80 000$ )进行记录。这里没有讨论透镜系统像差的放大倍率依赖性,讨论将限制在物体靠近物镜焦点的情况下。
在高倍率下,最终图像的质量是由第一个透镜(物镜)的像差决定,因为这里的散射角( $\theta_{0}$ )最大,球面像差(光线像差)取决于这个角的立方。由于后续镜头形成的图像更大,他们的角光谱(angular spectra)(衍射图案)更小。
另一个对高分辨率成像很重要的图像缺陷来自于电子不稳定性以及光束-样品相互作用,也成为色差。这是指光束中能量扩散的影响。后续会讨论射线像差和波像差之间的区别;这里只讨论像差的几何光学处理。对于表示为波像差或者相移(phase shift)的像差, $\theta_{0}$ 的指数增加一。
一个优雅的解决像差问题的方式是利用 Fermat’s principle 应用到光路 $W(P_{1}, P_{2})$ 的 $P_{1}$ 和 $P_{2}$ 这两点之间。以 $n$ 表示折射率,有
$$ W(P_{1}, P_{2}) = \int_{P_{1}}^{P_{2}}n\mathrm{d}s $$
根据 Fermat’s principle, 该函数是最小值或取平稳值(stationary value)。磁函数 $W(P_{1}, P_{2})$ 也称 Hamilton’s 点特征函数。将此函数展开为幂级数,可以展示出描述完美成像的完美成像的术语。偏离完美成像的偏差用更高阶的项来表示。这个理论远远超出了高分辨率的兴趣;但是,以下各部分总结了像差理论的主要结果,总结了像差校正(aberration-correction)的方法。
球面像差(spherical aberration)
球面像差的结果如图1所示,以大角度 $\theta_{0}$ 离开轴向物点的光线被透镜的外部区域折射相对较强,并被在高斯图像平面之前的汇聚。该平面满足方程,
$$ \frac{1}{U}+\frac{1}{V}=\frac{1}{f}\tag{S1} $$
其中近轴光线则由下方的近轴轴光线方程获得,并聚焦。
$$ \frac{\mathrm{d}^2r}{\mathrm{d}z^2} + \frac{e}{8mV_{r}}B^2_{z}r = 0 $$
像差射线的轨迹可以由全射线方程(full-ray equation)计算得出。
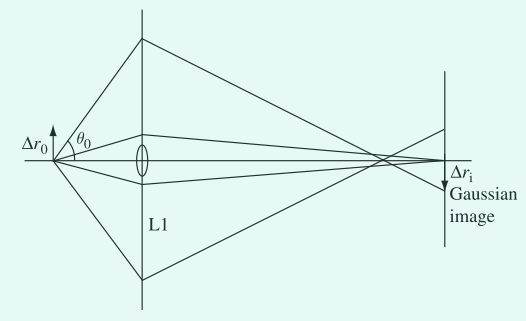
图1. 球面像差效果图。穿过透镜靠近外缘的射线相比更靠近光轴的射线折射更加强烈。这些外部射线会在高斯图像平面(Gaussion image plane)之前汇聚,并与高斯图像平面相较于距轴 $\Delta r_{i}$ 处。球面像差(或称光圈缺陷,aperture defect)是影响高分辨率图像质量的最重要缺陷。
如何考虑到来自轴向物点的所有光线,则最小直径的图像圆盘成为最小混淆圆(circle of least confusion)。距离 $\Delta r_{i}$ ,在高放大倍率的图像平面上与 $\theta_{0}^3$ 成正比。如果 $\Delta r_{i}$ 指的是物体空间,其与 $\theta_{0}^3$ 之间的比例常数,为三阶球差常数 $C_{s}$ (third-order spherical aberration constant)。即
$$ \begin{aligned} \Delta r_{0} &= C_{s}\theta_{0}^3 \\\ \Delta r_{i} &= MC_{s}\theta_{0}^3 = M^4\theta_{i}^3C_{s} \end{aligned} \tag{1} $$
最小混淆圆的半径为 $\frac{1}{4}C_{s}\theta_{0}^3$ 。 $C_{s}$ 的值取决于透镜激发和物体的位置,但对应于高倍率的情况,通常通过靠近物体焦平面的物体确定。在现代未经校正的仪器上, $C_{s}$ 的范围在 0.5 ~ 2.5 mm 之间,并为 “可解释” 的分辨能力设定了极限。 $C_{s}$ 的值可以从完整的(非近轴)方程的计算或者使用 Glaser(1956)给出的表达式获得。
对于第一种方法, Liebmann(1949)给出了简单的递归关系,表示真实轨迹与沿射线路径增量的近轴轨迹的偏差。如果平行于轴离开物体的近轴光线穿过轴的点处的偏差为 $\Delta$ ,则球面像差由下式给出,
$$ C_{s} = \Delta/\beta^3 \tag{2} $$
其中 $\beta$ 为图像焦点处近轴光线的斜率。
Glaser(1956)发现了 $C_{s}$ 的有用表达式,
$$ C_{\mathrm{s}}=\frac{e}{16 m_{0} V_{\mathrm{r}}} \int_{z_{1}}^{z_{2}}\left[\left\{\frac{\partial B_{z}(z)}{\partial z}\right\}^{2}+\frac{3 e}{8 m V_{\mathrm{r}}} B_{z}^{4}(z)-B_{z}^{2}(z)\left\{\frac{h^{\prime}(z)}{h(z)}\right\}^{2}\right] h^{4}(z) \mathrm{d} z \tag{3} $$
其中 $h(z)$ 是离开具有单位斜率的轴向物点的光线的近轴轨迹(paraxial trajectory)。 $eqn(3)$ 中导数的出现使得 $C_{\mathrm{s}}$ 的评估对场 $B_{z}(z)$ 的形状特别敏感。对于高分辨率,分辨率受 $C_{\mathrm{s}}$ 的限制, $eqn(3)$ 也展示了 $B_{z}(z)$ 的详细形式,以及极片的形状,敏感地决定了仪器的分辨率。因此在处理极片时必须要格外小心。
五阶球面像差项 $C_{5}$ 在非常高的分辨率下也可能很重要。例如,已经发现在 100 kV 时, $C_{\mathrm{s}} = 0.5 mm$ ,对于小于 0.1 nm 的间距, $C_{5}$ 的影响不能忽略不计。
色差(Chromatic aberration)
色差源自于对于所用射线波长的依赖性,因此与电子能力相关。使用多色照明,在一组平面上形成聚焦图像(in-focus images),每个平面对应着照明射线中存在的每个波长。
现代仪器中存在三个重要的波长波动来源。对于高分辨率下使用的薄样品( t < 10 nm ),这些按重要性降序排序:
- 离开灯丝的电子的能量扩散:在高枪偏压设置( high gun-bias setting )下,有 $\Delta E/E_{0} = 10^{-5}$ 。
- 高压不稳定型( High-voltage instabilities ): 典型的波动规格为 $\Delta V_{0}/V_{0} = 2 \times 10^{-6}/min$ ,其中 $V_{0}$ 为显微镜高压。
- 样品中的能量损失。
在色差常数 $C_{c}$ 的定义中包含高压电源和物镜电流的波动较为方便,
$$ \frac{1}{f} = \frac{A_{0}(NI)^2}{V_{r}(S + D)} $$
上等式的微分给出,
$$ \frac{\Delta f}{f} = \frac{\Delta V_{0}}{V_{0}} - \frac{2\Delta B}{B} = \frac{\Delta V_{0}}{V_{0}} - \frac{2\Delta I}{I}\tag{4} $$
为了偏离薄透镜定律( $eqn(S1)$ ), $eqn(4)$ 中引入比例常数 $K$ 。 色差常数 $C_{\mathrm{c}}$ 定义为 $C_{\mathrm{c}}=Kf$ ,所以有
$$ \begin{aligned} \Delta f & = C_{\mathrm{c}}\left(\frac{\Delta V_{0}}{V_{0}} - \frac{2\Delta B}{B}\right) \\ & = C_{\mathrm{c}}\left(\frac{\Delta V_{0}}{V_{0}} - \frac{2\Delta I}{I}\right) \\ \end{aligned}\tag{5} $$
实践中,透镜电流和高电压的波动不太可能相关,因此焦距的随机波动应该从统计理论中的方差操作规则中获得。添加正交波动(fluctuations in quadrature)给出方差,
$$ \frac{\sigma(f)}{(f)}=\left[\frac{\sigma^2(V_{0})}{V_{0}^2} + \frac{4\sigma^2(I)}{I^2}\right]^{1/2}=\Delta/C_{\mathrm{c}}\tag{6} $$
$I$ 和 $V_{0}$ 的方差必须通过测量获得,或者可以通过将 $\Delta$ 作为拟合参数或从衍射图分析推导出它们的值。
现在使用几何光学方法作为第一近似值来确定焦距的微小变化对图像的影响。透镜具有较长焦距的能量稍高的射线被带到距离高斯像平面的焦距 $\Delta V$ 处,其中
$$ \Delta r_{i} = \Delta V\theta_{i}\tag{S2} $$
微分透镜方程
$$ \frac{1}{U} + \frac{1}{V} = \frac{1}{f} $$
可以得到
$$ \begin{aligned} \mathrm{d}\left(\frac{1}{U}\right) & = \mathrm{d}\left(\frac{1}{f}\right) - \mathrm{d}\left(\frac{1}{V}\right) \\ 0 & = \frac{-1}{f^2}\mathrm{d}f + \frac{1}{V^2}\mathrm{d}V \\ \frac{\mathrm{d}V}{\mathrm{d}f} & = \left(\frac{V}{f}\right)^2 \approx M^2 \\ \end{aligned} $$
这样有以下关系式,
$$ \Delta V = M^2\Delta f \tag{7} $$
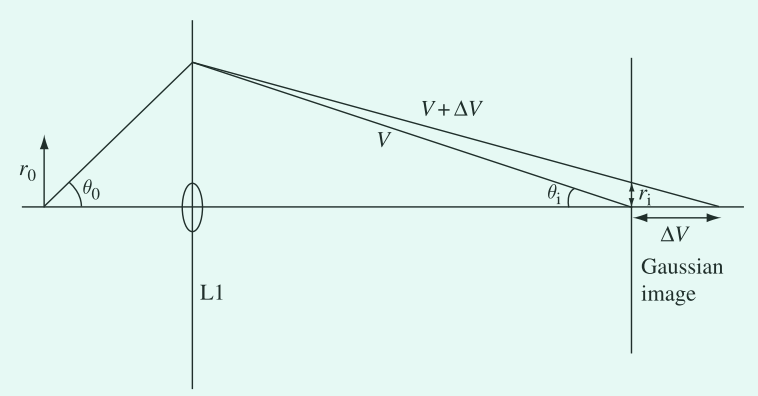
图2. 色差的影响,通过势 $V+\Delta V$ 加速的快速电子比通过势 $V$ 加速的相对低能量电子的折射的角度更小。这些更高能量的电子被带到了高斯成像平面上,在距轴 $r_{i}$ 处通过。
根据 $eqn(S2)$ 有
$$ \Delta r_{i}=M^2\Delta f\theta_{i} $$
参照物空间,轴向物点的扩展圆盘图像(extended disc image)具有半径,
$$ \begin{aligned} \Delta r_{0} &= \frac{1}{M}\Delta r_{i} \\\ &=M\Delta f\theta_{i} \end{aligned} $$
由角放大率公式
$$ \frac{\tan\theta_{i}}{\tan\theta_{0}}\approx\frac{\theta_{i}}{\theta_{0}}=\left|\frac{1}{M}\right| $$
得到
$$ \Delta r_{0}=\theta_{0}\Delta f $$
通过 $eqn(5)$ ,
$$ \Delta r_{0} =\theta_{0}C_{\mathrm{c}}\left(\frac{\Delta V_{0}}{V_{0}} - \frac{2\Delta I}{I}\right)\tag{8} $$
例如,样品的图像中引入了 25 eV 离散能量损失。许多生物样本在这种能量下显示出相当宽的峰值。损失电子后的图像将会以物平面为基准 $\Delta U$ 。在高放大倍率下,根据透镜方程可以得到,
$$ \Delta U \approx \Delta f \tag{9} $$
因此,当忽略透镜电流的波动,可以从 $eqn(5)$ 获得损失图像的聚焦缺陷。对于 $C_{\mathrm{c}} = 1.6 mm$ 以及 $\Delta E = 25 eV$ , 100 keV 时 $\Delta U = 400 nm$ 。由于对于损失电子的情况,透镜的焦距较短, $V$ 固定的情况下,不得不通过削弱聚焦在弹性图像的物镜电流,使得非弹性图像在聚焦在焦距以内。这样非弹性像损失会出现在图像欠焦的情况,这时第一菲涅尔条纹(Fresenl fringe)会显得很亮,这时透镜的电流太弱。不幸的是,对于高分辨率的相位衬度,会出现在聚焦不足的情况(在 100 kV 下约为 90 nm),使得任何非弹性的贡献在弹性图像中表现为过焦背景模糊。对于许多样品,总的非弹性图像贡献可能超过弹性贡献。
实践中,一旦场分布已知, $C_{\mathrm{c}}$ 可以使用
$$ C_{\mathrm{c}} = \frac{e}{8mV_{r}}\int_{z_{1}}^{z_{2}}B_{z}^2(z)h^2(z)\mathrm{d}z \tag{10} $$
来表示。其中 $h(z)$ 使用 $eqn(3)$ 中的函数。原则上可以通过将磁透镜与静电镜组合来消除色差,因为静电镜的色差符号与磁透镜是相反的。
$C_{\mathrm{c}}$ 可以通过用高电压或者透镜电流测量焦距变化来实验测量。如果样品后为使用透镜,则 STEM 一起不存在色差。后续会介绍也可以用波光学表示色差问题,应该强调 $eqn(8)$ 是一种几何近似,对于中等散焦的点目标的空间非相干成像,即 $\Delta V$ 不太小的情况时是精确地。对于小 $\Delta V$ 或者相干照明(或者两种情况同时),则必须使用波光学方法。
像散(Astigmatism)
严重的像散是由不对称的磁场引起的。可以通过将弱柱面透镜(cylindrical lens)叠加在完全对称的透镜上来表示透镜场中与完美对称的背离。下图展示了由像散透镜形成的点的图像,作为在光轴上不同点的两条线焦点(line foci)。
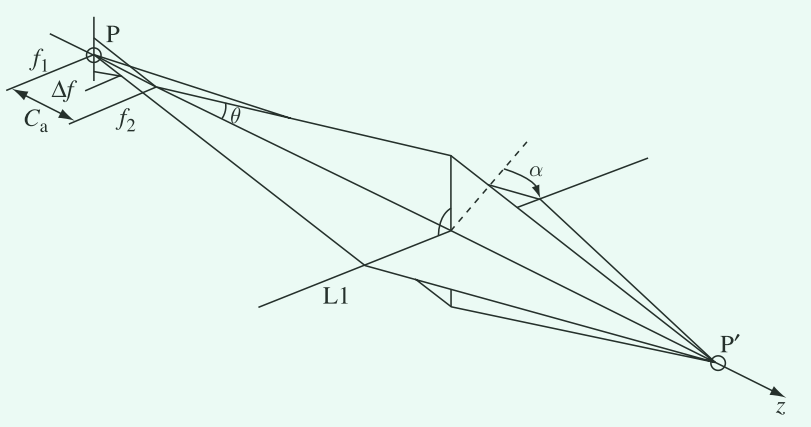
图3. 像散。镜头的焦距取决于光线离开物体的方位角 $\alpha$ (azimuthal angle, $\alpha$ )。这些光线位于包含光轴的平面中。展示了最大和最小焦距的直角平面,平均焦距为 $f$ 。最大焦点和最小焦点之间的差异即为像散常数 $C_{\mathrm{a}}$ 。
像散可以认为是一个与方位角相关的焦距,它产生以下公式中的相移动,
$$ \chi_{4}(\theta)=\frac{2\pi}{\lambda}\left(\frac{1}{4}C_{\mathrm{a}}\theta^2\sin{2\phi}\right) $$
后续会讨论测量像散常数 $z_{a}$ 的原位( In situ )方法。经验丰富的操作员使用配备由像散器的现代仪器来进行矫正像散,可以减少这种像差,从而不会对分辨率造成限制;然而,这需要大量练习。像散器是一种弱四极透镜(weak quadrupole lens),其激发由电子控制,以通过引入具有正确强度和方向的补偿弱柱面透镜(compensating weak cylindrical lens)来校正任何方向的场不对称性。
物镜极片的椭圆度(ovality)需要几微米的加工公差(machining tolerance)以使得像散在易于矫正的范围内。所用铁的均匀性(homogeneity)非常重要。
最近分辨率提高到亚埃级(sub-angstrom level)已经暴露了三倍像散(three-fold astigmatism)。 在 Overwijk(1997) 等人的论文中可以找到其测量和删除的示例。 后续波动光学部分,将从波动光学的角度讨论二重和三重像散。