参考 John C. H. Spence 著作的 《High-Resolution Electron Microscopy》(Fourth Edition, Oxford university press)。
1. 近轴射线方程(The paraxial ray equation)
1.1 磁场力
1.1.1 安培力
磁场力分为安培力与洛伦兹力,安培力的公式为
$$ F = ILB\sin{\alpha} $$
其中 $\alpha$ 代表 $(I, B)$ 是电流方向与磁场方向的夹角。安培力是通电导线在磁场中受到的作用力。
1.1.2 洛伦兹力
洛伦兹力公式为
$$ F = q(E + v\times B) $$
其中 $F$ 表示为洛伦兹力,$q$ 是带电粒子的电荷量,$E$ 代表电场强度,$v$ 代表带电粒子的速度,而 $B$ 代表磁感应强度。洛伦兹力是运动电荷在磁场中所受到的力,即磁场对运动电荷的作用力。当只考虑磁场部分时,我们有
$$ F = qv \times B \tag{1} $$
因受力方向与运动方向垂直,故不做功,只改运动方向。当定义为所有的电磁力,则需要包括电场部分。电场部分有可能做功。
PS:该公式为基本公式,不是从其他公式推到得到。
1.1.3 磁场力的方向判断
左手定则
主要用来判断力的方向,包括洛伦兹力和安培力。
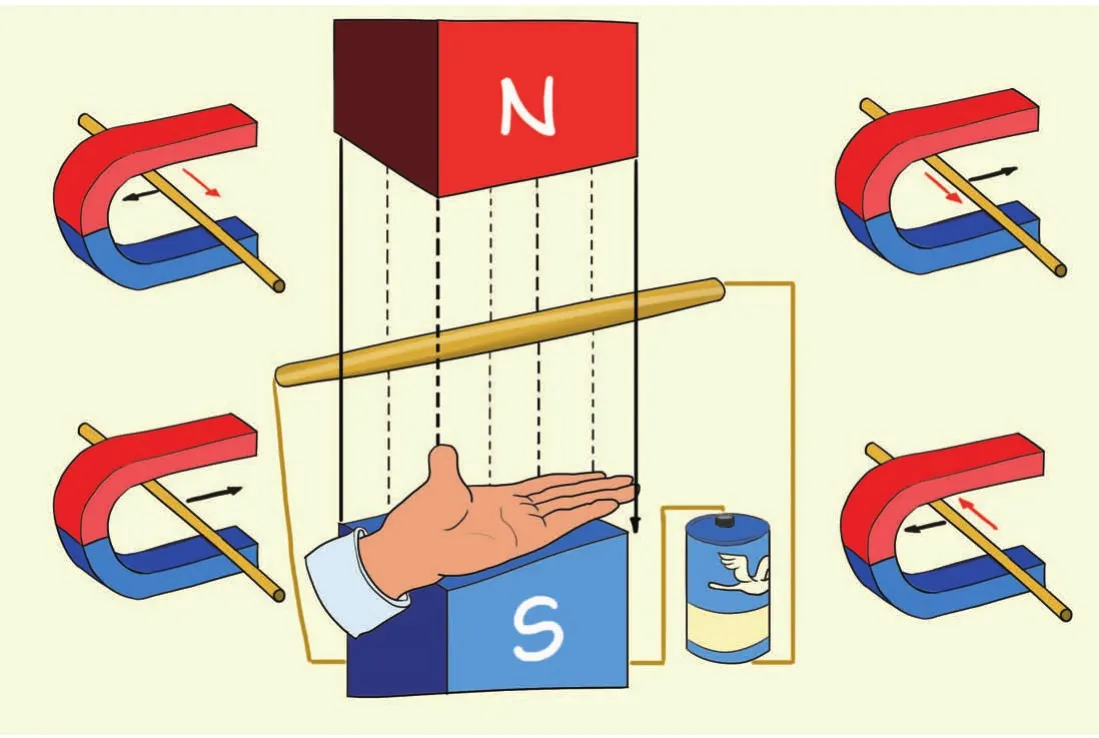
图S1. 左手平展,让磁感线穿过手心,使大拇指与其余四指垂直,并且都跟手掌在一个平面内。把左手放入磁场中,让磁感线垂直传入手心,手心面向 $N$ 极,四指指向电流所指方向,则大拇指的方向就是导体受力的方向。
1.2 极片(pole-piece)构造
轴对称磁场的聚焦作用可以理解如下。图1中为电子透镜的简化图,包括典型的磁通量线。极片(pole-piece)尺寸 $S$,$R_1$,以及 $R_2$ 在图中显示。
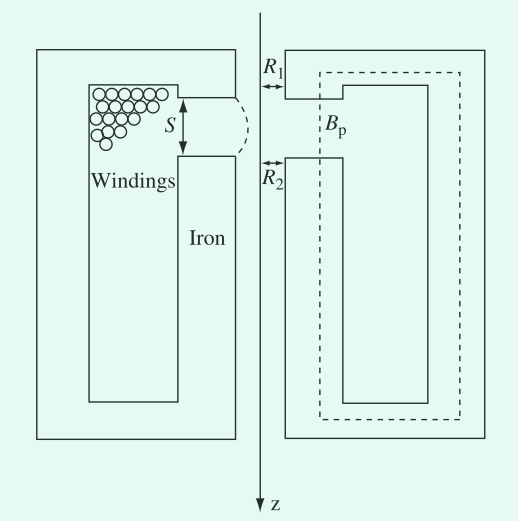
图1. 磁电子透镜的简化图。极片尺寸已经表明,安培定律的路径显示为虚线。磁通量线也被显示为虚线,从而定性地指示了镜头的聚焦作用。远离光轴间隙中的场强标记为 $B_p$。实际使用中,绕组(winding)是水冷的,并且极片是可拆卸的。
透镜极片的重要区域的实际布置见图2。
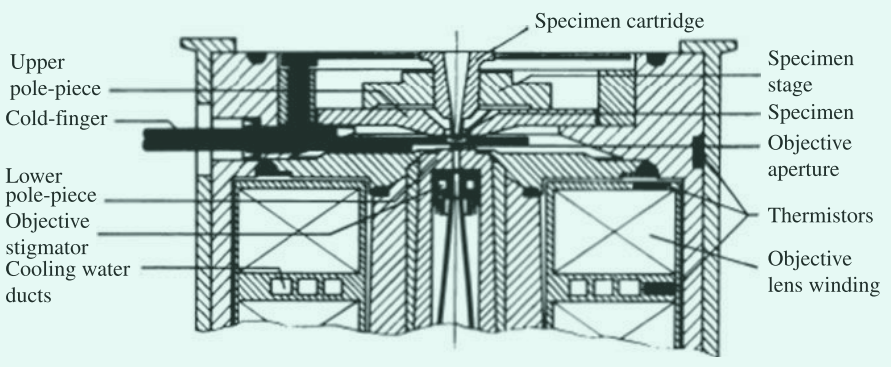
图2. 实际中高分辨率极片的细节。在这种商业设计中,上极片孔径 $2R1$ 为 9 mm,下极片孔径 $2R2$ 为 3 mm,间隙 $S$ 为 5 mm。近轴射线方程
1.3 电子在极片中的运动轨迹
磁场 $B$ 被限制在极片的间隙内,在这里,带有 $-e$ 、速度为 $v$ 的电子受力为
结合牛顿第二定律,$F = ma = m\frac{d^2r}{dt^2}$
$$ F = -ev \times B = m\frac{d^2r}{dt^2} \tag{2} $$
$F$ 的方向遵循左手则(电流方向与电子方向相反),如图1所示,当电子进入左侧场时,左手定则进入纸面(假设上极片为北极)。相反的,如果电子从右侧场进入场,则左手定则外出纸面。这样会导致电子沿螺旋轨迹前进。施加的旋转速度分量 $r_\theta$ 与场 $B_z(r)$ 的 $z$ 方向分量相互作用产生朝向轴方向的力,同样由左手定则给出。这个力控制着透镜的聚焦行为。
关于极板,找到了两张感觉更好点的图,如图3,4。
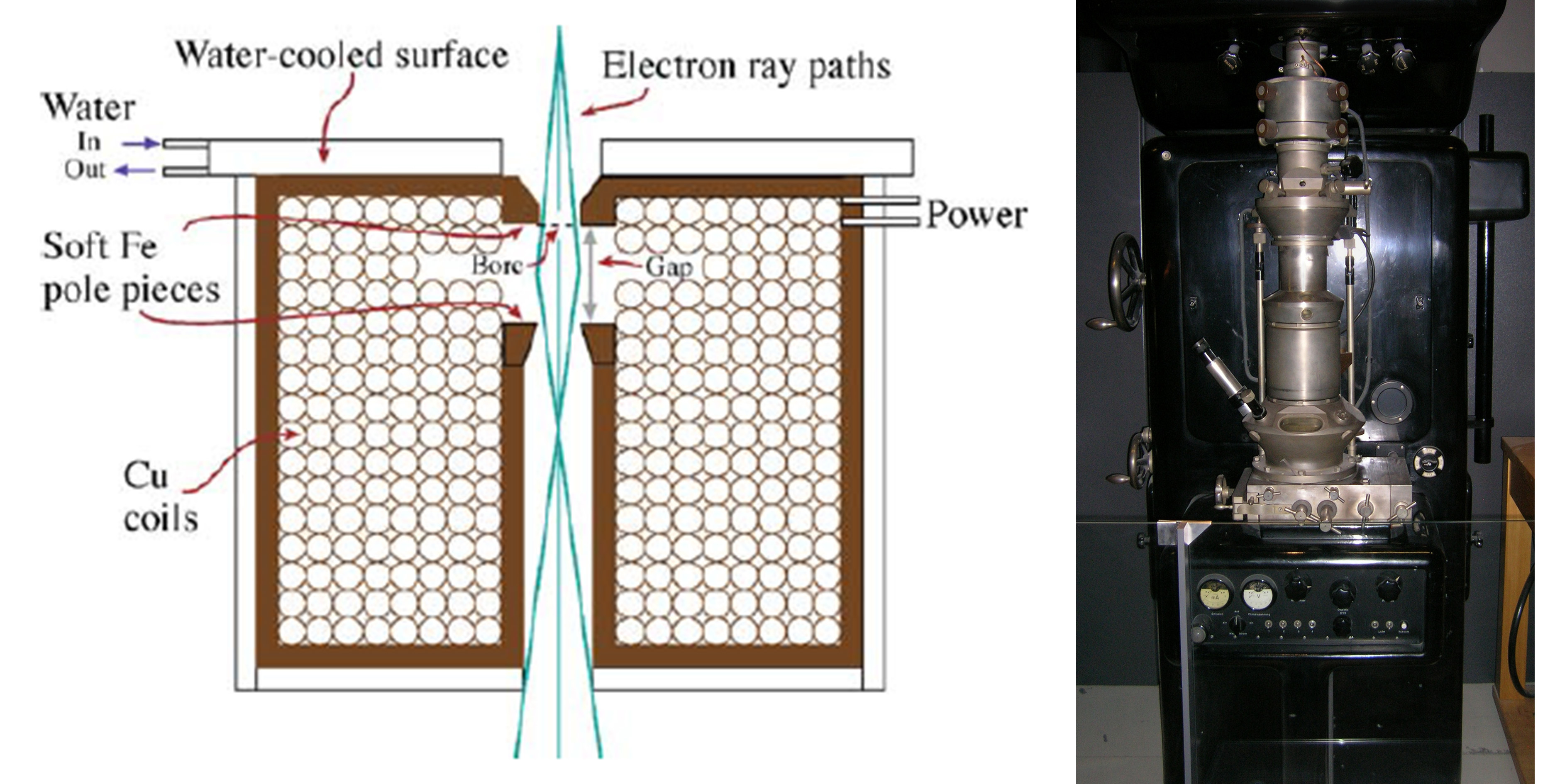
图3.
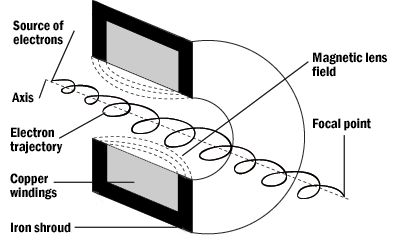
图4
使用其他光学课本中的一些估计值,$eqn(2)$ 可以简化为柱坐标系(cylindrical coordinate system)中的子午线(meridional rays)。这些是到达透镜前包含轴的平面中的光线。这一简化过程包括忽略掉会导致不完美成像(镜头像差, lens aberrations)的项。近轴射线方程中仅包含在光轴 $B_z(z)$ 方向评估的磁场的 $z$ 组分分量。简化后的图像为:
$$ \frac{d^2r}{dz^2} + \frac{e}{8mV_r}B_z^2(z)r = 0 \tag{3} $$
其中 $r$ 是电子到光轴的径向距离,$V_r$ 是相对论修正后的加速电压。一旦轴上的场 $B_z(z)$ 已知,就可以通过计算 $eqn(3)$ 追踪单个电子进入场中的轨迹。对于对称透镜,平行于轴进入的电子射线将定义后续所有电子透镜的参数。需要注意的是,这里已经进行了场的 $z$ 分量不依赖于 $r$。
$eqn(3)$ 是具有两个线性独立解的二阶线性微分方程,描述的满足完美透镜行为的射线。通过计算 $eqn(2)$ 可以求解特定磁场中电子的轨迹。通过将这些真实的电子轨迹与满足 $eqn(3)$ 的理想电子轨迹进行比较(并生成完美成像),这使得求解这个磁透镜的像差变为可能。或者,利用 $eqn(3)$ 的解的函数关系式给出的各种像差系数简单的表达式也同样能够给出。
注:柱坐标系,示意图如下
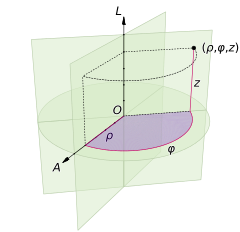
图5. 一个以 $O$ 为原点、$A$ 为极轴、$L$ 为纵轴的柱坐标系。其中标出的点的径向距离 $\rho=4$ ,角坐标 $\varphi = 130°$,高度 $z=4$。
其中坐标系规定如下:
$$ \begin{aligned} x & = \rho\cos{\varphi} \\ y & = \rho\sin{\varphi} \\ z & = z \end{aligned} $$
$$ \varphi= \begin{cases}0 & \text { if } x=0 \text { and } y=0 \\ \arcsin \left(\frac{y}{\rho}\right) & \text { if } x \geq 0 \\ \arctan \left(\frac{y}{x}\right) & \text { if } x>0 \\ -\arcsin \left(\frac{y}{\rho}\right)+\pi & \text { if } x<0 \end{cases} $$

图6. 柱坐标面。三个正交分量,$\rho$ (绿色)、$\varphi$ (红色)、$z$ (蓝色),图中每个分量都以恒定速率增加。该点位于三个彩色表面之间的交点处。
相似的,也能够得到子午线的螺旋旋转方程。在这个平面的旋转可以用以下关系给出,
$$ \theta_0 = \left(\frac{e}{8mV_r}\right)^{1/2}\int_{z_1}^{z_2}B_z(z)dz \tag{4} $$
通过经向平面(或子午平面,meridional plane)进入透镜的射线保持在该平面中,当射线穿过透镜场时,该平面旋转 $\theta_0$ 。注意由于图像反转( $M < 0$ ),总图像旋转为( $180+\theta_0$ )度。
可以看出,图1中所示的透镜非常低效,因为大部分损耗的功率用于支持 $z$ 方向上的场,这对平行于轴进入的电子没有产生任何力。像差矫正器使用效率更高的六极杆(hexapoles)或者四级杆(quadrupoles)。
2. 常场近似(The constant-field approximation)
$eqn(3)$ 如在可以忽略掉场对于 $z$ 的依赖性会变得很容易求解。它类似于谐波运动的微分方程,并且这种“常场”近似的准确性很高,与中等和弱激发下投影仪镜头焦距的实验非常吻合。这里介绍恒定场近似是为了洞察磁透镜的物理特性。由于 $Cs$ 表达式涉及到求解场的导数,不能期望使用这样的粗略模型来理解像差的影响。
如果坐标的原点位于极片间隙(长度为 $S$ )中间的平面上,则 $z$ 方向上的场常数由以下给出,
$$ B_{z}(z) \begin{cases} =B_{p} & \text { for }-S / 2 \leq z \leq S / 2 \\ =0 & \text { elsewhere } \end{cases} \tag{5} $$
$eqn(3)$ 可以简化为,
$$ \frac{d^2r}{dz^2} + k^2r = 0 \tag{6} $$
其中
$$ k^2 = \left(\frac{e}{8m_0V_r}\right)B_p^2 \tag{7} $$
带入数值运算得到,
$$ k = 1.4827 \times 10^5 B_p/V_r^{1/2} $$
$B_p$ 单位为特斯拉,$V_r$ 单位为瓦特。$eqn(6)$ 的公式的解为
$$ r = A\cos{kz} + B\sin{kz} \tag{8} $$
其中 $A$ 与 $B$ 为由边界条件确定的常数。对于使透镜平行于轴的射线,在 $z = S/2$ 处匹配斜率与纵坐标 $r_0$ ,可以得到
$$ \begin{cases} r = r_{0} & z = 0 \\ \mathrm{d}r/\mathrm{d}z = 0 & z = S/2 \\ \end{cases} $$
推论出下式同时满足 $eqn(6)$ 以及上式,
$$ r = r_0\cos{k(z - S/2)} \tag{9} $$
利用安培定律,可以得到,“常场” 的强度 $B_p$ 与匝数(number of turns)以及透镜的电流 $I$ 相关联。
如果透镜 $D$ 的孔径足够小,不会干扰磁路,并且铁的磁阻相比于间隙 $S$ 的磁阻可以忽略不计。对于图1的电路,我们有
$$ B_p = \frac{\mu_0NI}{S} = 4\pi \times 10^{-7}\left(\frac{NI}{S}\right) \tag{10} $$
其中 $I$ 的单位为安培,$B_p$ 的单位为特斯拉。注意到,如果在距离光轴足够远的地方进行测量,$B_p$ 可以作为给出任何透镜间隙中的通量密度(flux density)的参数。