参考 John C. H. Spence 著作的 《High-Resolution Electron Microscopy》(Fourth Edition, Oxford university press)。
投影透镜(The projector lens)
投影透镜的概念
将前一个透镜所成像作为成像物体的镜头,例如图1中的 $L2$,$L3$ 以及 $L4$ 透镜,被成为投影透镜。中间镜 属于投影透镜这一类,以区别于使用物理标本样品作为成像物体的透镜。
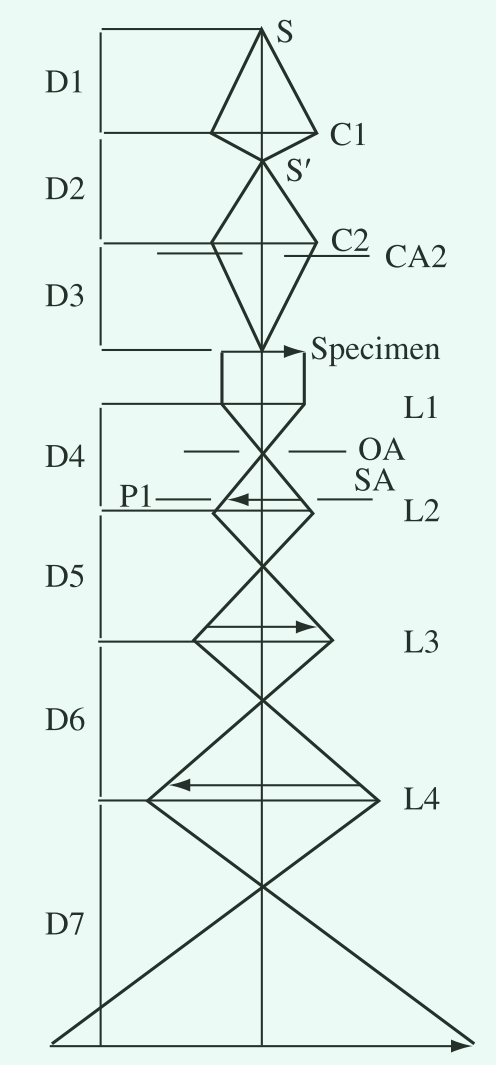
图1. 在高放大倍率下使用的,具有两个聚光透镜(condenser lenses),$C1$ 和 $C2$,以及四个成像透镜,$L1$,$L2$ 和 $L3$ 的电子显微镜示意图。其中 $L2$,$L3$ 以及 $L3$ 为投影透镜。$OA$ 是物镜孔径,$P1$ 是固定平面,$SA$ 是选定区域的孔径。
例如,由 $L2$ 形成的像会出现在 $L3$ 的透镜内,作为新的成像对象。如果该像被 $L3$ 作为新的成像目标,那么可以通过”简单透镜特点”部分中提及的构造找到 $L3$ 所形成的图像。当移除 $L3$ ,或者当 $L2$ 形成的像超出了 $L3$ 的中心,则会观察到 $L2$ 所形成的像。
投影透镜中的电子轨迹参数
之前博文所提及的公式,
$$ r = r_{0}\cos{k(z-S/2)} \tag{1} $$
给出表征透镜内真实电子运动轨迹行为的简单模型。现在用这个方程找出等效理想透镜的焦距和主平面位置。然后可以利用理想透镜构造的连续应用找到透镜系统所形成的像。
投影对象焦点 $f_{p}$ 可能会落在透镜视野之内或之外,如图2所示。
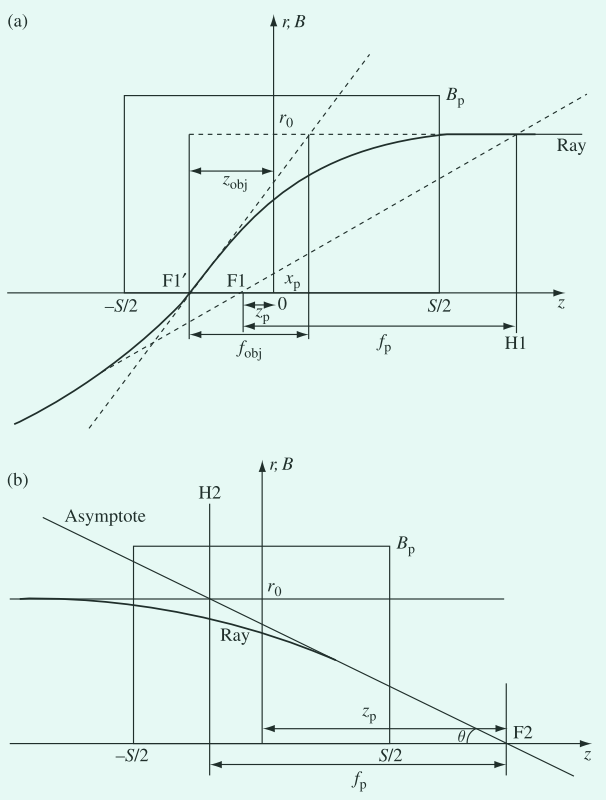
图2. (a)物镜与投影透镜焦距(focal length) $f_{obj}$ 和 $f_{p}$ 的定义。同时图中还标注了对焦距离(focal distance),物镜与投影透镜的对焦距离分别表示为 $z_{obj}$ 以及 $z_{p}$ 。物镜样品放置于靠近 $F1’$ 的位置。此图显示了当焦点位于透镜场内部时,透镜同时被用作物镜(焦点在 $F1’$)及用作投影镜(焦点位于 $F1$)。(b)投影透镜的线路图,焦点位于透镜场外(从 $-S/2$ 至 $S/2$ )。纵坐标表示场强和光线到光轴的距离。图像焦点为 $F2$ 。Asymptote,渐近线。
使用 $z\rightarrow\infty$ 来表示渐近线方向上的延伸,用来定义“虚拟”或者渐进投影焦距 $f_{p}$ 。图2中主平面与物焦点之间的距离可以表示为,
$$ \begin{aligned} f_{p} & = r_{0}/\tan{\theta} \\ & = r_{0}/\left(\frac{\mathrm{d}r}{\mathrm{d}z}\right)_{-\infty} \\ & = r_{0}/\left(\frac{\mathrm{d}r}{\mathrm{d}z}\right)_{-S/2} \end{aligned}\tag{2} $$
由 $eqn(1)$ 及 $eqn(2)$ 公式可以推导出,当 $z = -S/2$ 时,
$$ f_p/S = [Sk\sin{(Sk)}]^{-1} \tag{3} $$
该函数于图3中画出,展示了投影透镜的最小焦距特征。透镜通常在 $0 \lt Sk\lt 2$ 范围内工作,尽管已经对使用 $Sk > 2$ 的“第二区”透镜的性质进行了高分辨率的研究。$eqn(3)$ 给出了 $f_{p}$ 最小值 $0.56S$。
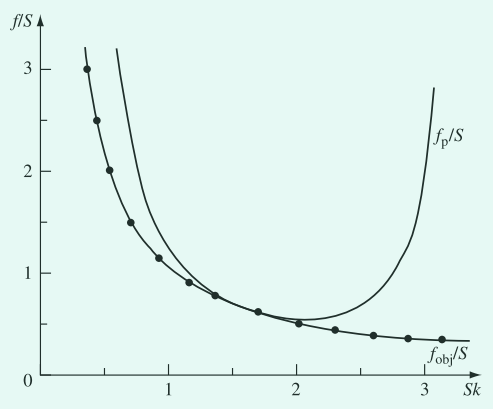
图3. 对于常场模型,物镜与投影透镜的相对焦距( $f_{obj}$ 及 $f_{p}$ )作为透镜激发(与电流成比例)的函数。投影透镜的最小焦距出现在 $f_{p} = 0.56S$ ,其中 $S$ 是极片间隙大小。
利用之前的公式,
$$ B_{p} = \frac{\mu_{0}NI}{S} = 4\pi \times10^{-10}\left(\frac{NI}{S}\right)\tag{*} $$
以及
$$ k = 1.4827 \times 10^5 B_p / V_r^{1/2} $$
将 $Sk$ 带入上两式,约去 S,得到图3中的横坐标 $Sk$ 在常场估计中有,
$$ Sk= 0.1862\left(\frac{NI}{\sqrt{V_{r}}}\right) \tag{4} $$
物体焦距 $z_{p}$ 定义为透镜中心与物体焦点之间的距离。从图1(a)中可以看出,与 $f_{p}$ 一起定义了主平面的位置。从图2(b)中得,
$$ z_{p} = S/2 - r(-S/2)/\left(\frac{\mathrm{d}r}{\mathrm{d}z}\right)_{-S/2} $$
由 $eqn(1)$,
$$ \frac{Z_p}{S} = \left(\frac{1}{2}-\frac{1}{kS\tan{kS}}\right) \tag{5} $$
当公式用于投影透镜时,如图2(b),符号是相反的,即此时的 $z_{p}$ 为负。
$$ S/f_{p} = (Sk)^2 \tag{6} $$
当忽略主平面之间的距离时,这是“薄”磁透镜的公式。 Busch (1926) 在最早的一篇关于电子光学的论文中获得了这个结果的稍微更一般的形式。 他的结果是通过对 $eqn(7)$ 进行积分获得的, $$ \frac{\mathrm{d}^2r}{\mathrm{d}z^2} + \frac{e}{8mV_{r}}B_{z}^2(z)r=0\tag{7} $$
假设 $r$ 在透镜场内是常数,然后有
$$ \frac{1}{f_{p}}=\frac{e}{8mV_{r}}\int_{-\infty}^{\infty}H_{z}^2(z)\mathrm{d}z \tag{8} $$
对于“高帽场”(“top-hat” field) $eqn(8)$ 与 $eqn(6)$ 一致。
为了在一条通用曲线上表达所有磁透镜的焦点特性,Liebmann (1955) 发现有限孔径 $D$ 的透镜可以用 $eqn(8)$ 的修改形式来描述:
$$ \frac{1}{f} = \frac{A_{0}(NI)^2}{V_{r}(S+D)}\tag{9} $$
其中 $A_{0}$ 近似为常数。这对于弱激发透镜是一个很好的近似,并且可以通过取
$$ D = R_{1} + R_{2} $$
来扩展到包括非对称透镜。
不幸运的是,强透镜的特性对于极片几何形状的细节越来越敏感,使得 $eqn(9)$ 变得非常不可靠。特别地,由于现代物镜的焦距与极片尺寸对比并不大,因此这些镜头不能被视为“薄”透镜。
关于强弱磁透镜定义的补充
网上找了很久才找到一些描述。
弱磁透镜(weak lens),弱压短透镜,长焦,放大倍数可调节 0 ~ 20倍。如中间镜。功能包括控制电镜总放大倍数,成像/衍射模式选择。
强磁透镜(Strong lens),短焦、强磁透镜,进一步放大中间镜的像。如投影镜,内孔径较小,使电子束进入投影镜孔径角很小。功能包括,景深大,改变中间镜放大倍数,使总倍数变化大,也不影响图像清晰度。焦深长,放宽对荧光屏和底片平面严格位置要求。有些电镜还装有附加投影镜,用以自动校正磁转角。
关于对称透镜与非对称透镜定义的补充
如果一个透镜的两个圆弧半径相等,则称为对称透镜(symmetric lens),否则称为非对称透镜(asymmetric lens)。双鱼囊(vesica piscis,间图5)是对称透镜的一种形式,由两个圆的弧组成,每个圆的中心位于相反的弧上。圆弧在其端点处以 120° 的角度相交。
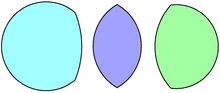
图4. 非对称透镜(左右)及对称透镜(中间)
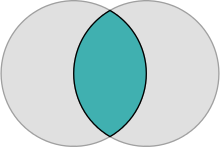
图5. 双鱼囊(Vesica piscis)是两个圆盘的交点,两个圆盘具有相投的半径 $R$ ,并且中心之间的距离也等于 $R$ 。
对称透镜的面积可以而用半径( $R$ )和弧长( $\theta$ )以弧度表示为,
$$ A = R^2(\theta - \sin{\theta}) $$
非对称透镜的面积则由半径( $R$ , $r$ )以及两者中心之间距离( $d$ )给出,
$$ A = r^2\cos^{-1}{\left(\frac{d^2 + r^2 - R^2}{2dr}\right)} + R^2\cos^{-1}{\left(\frac{d^2 + R^2 - r^2}{2dR}\right)} - 2\Delta $$
其中 $\Delta$ 为三边分别为 $d$ ,$r$ 以及 $R$ 。
$$ \Delta = \frac{1}{4}\sqrt{(-d + r + R)(d - r + R)(d + r - R)(d + r + R)} $$
如果 $d \lt r + R$ 两个圆圈发生重叠,当 $d$ 足够大时,透镜的中心位于两个圆中心之间。如下图6,
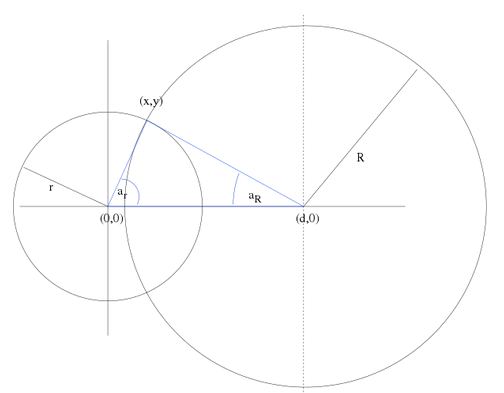
图6. 透镜中心位于两圆中心之间的情况。
如果 $d$ 比较小的情况,透镜中心位于连接两圆中心线段外侧。如图7,
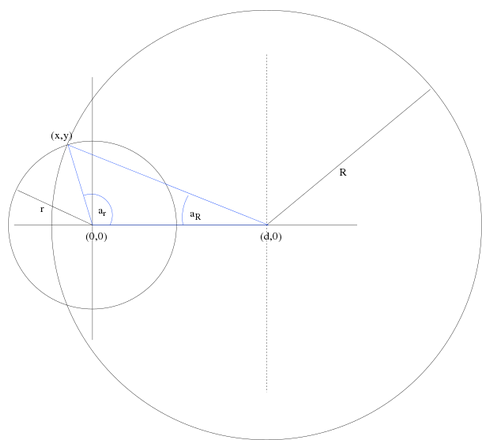
图7. 透镜中心位于两圆中心之间外侧的情况。
物镜(The objective lens)
物镜紧挨着样品,是显微镜的核心。由于角放大率( $m$ )与横向放大率( $M$ )成反比,
$$ m = \frac{\tan{\theta_{i}}}{\tan{\theta_{0}}} \approx \frac{\theta_{i}}{\theta_{0}} = \left|\frac{1}{M}\right| $$
透镜提供的放大率能够确保射线以非常小的角度进入到所有后续透镜的光轴。透镜的像差随着角度的增加而急剧增加,所以正是物镜中光线与光轴的角度最大,决定了最终成像的质量。
最重要的透镜像差由像差常数 $C_{c}$ 以及 $C_{s}$ 指定,他们与透镜的焦距非常接近。对于高分辨率电镜,减少像差是非常重要的,通过将样品引入物镜场可以减少焦距和透镜像差,这种设计被成为 侵入式透镜(immersion lens)。
保持在物体照明侧的场成为 前场 (pre-field),它对于图像的形成不发挥任何作用。可用于成像的剩余区域的范围取决于目标样品的位置。因此,透镜主平面的位置和像差系数取决于物体的位置 $z_{obj}$ ,其成为了这些透镜的重要电子光学参数。
$z_{obj}$ 是从透镜的中心测量的,按照惯例,其与物镜焦距 $f_{obj}$ 是为产生无限远(无限放大)图像的透镜而指定的,以便样品处于精确的物体焦点处。 $z_{obj}$ 也因此等于物焦距。
$$ k^2 = \left(\frac{e}{8m_{0}V_{r}}\right)B_{p}^2 $$
对于由以上公式描述的简单透镜,从对称性中看出像和物焦距是相等的是很容易的。这些由分别平行于轴进入和离开的射线定义。因此可以从以下公式
$$ r = r_{0}\cos{k(z-S/2)} $$
看出,当余弦参数为 $-\pi/2$ 时,纵坐标为零。即
$$ \begin{aligned} k(z-S/2) &= -\frac{\pi}{2} \\ z &= \frac{\pi}{2k}-\frac{S}{2} \end{aligned} $$
所以有
$$ \begin{aligned} \frac{z_{obj}}{S} &= \frac{\lvert z \rvert}{S} \\ &= -\left(\frac{\pi}{2kS} - \frac{1}{2}\right) \\ \end{aligned}\tag{10} $$
而真正的焦距 $f_{obj}$ 为
$$ f_{obj} = r_{0}/\left(\frac{\mathrm{d}r}{\mathrm{d}z}\right)_{z_{obj}} \tag{11} $$
得出
$$ \frac{f_{obj}}{S} = (Sk)^{-1}\tag{12} $$
正如图3所示的 $f_{obj}/S$ 曲线所示。与 $eqn(3)$ 相比,
$$ \frac{f_{p}}{S} = [Sk\sin{(Sk)}]^{-1}\tag{3} $$
表明用作物镜的透镜焦距可能比用于投影镜的焦距短。实际上,焦距的下限是根据透镜极片的饱和度设定的。
物镜的数据,包括下一部分,实际透镜设计中,根据透镜激发与 $z_{obj}$ 绘制的图。 解释如下,对于指定的激发,纵坐标给出了在无穷远处产生图像所需的物体位置。这将是在高放大倍率下操作的透镜的近似样本位置。物体然后通过焦距与物体主平面分开,并且通常放置于透镜的照明侧。
对于高激发状态下的非对称物镜( $R_{1}\neq R_{2}$ ),焦距取决于 $R_{1}$ 或 $R_{2}$ 中的哪一个在像空间中。对于较弱的透镜,情况并非如此。高度不对称的物镜在现代显微镜中很受欢迎,因为必须适应样品更换机制,所以在顶部入口阶段,样品从上方引入。 对于倾斜台(tilt stage), $2R_{1}$ 的典型值大约为 20 mm,而 $2R_{2}$ 可能小至 2 mm。极片不对称的影响是会增加 $B_{z}(z)$ 的最大值( $R_{1}$ 和 $S$ 保持不变)并将最大值对应的位置移向较小的极片 ( $R_{2}$ )。 对于 $R_{2}\rightarrow0$ ,该最大值与消失的极片面一致。对于真实的透镜, $B_{z}(z)$ 是一个平滑的峰值函数,透镜重要的折射效应发生在场的最大值附近。Liebmann 能够通过模拟计算,表明非对称透镜的最大值与极片直径 $D=R_{1}+R_{2}$ 的等效对称透镜(equivalent symmetrical lens)的最大值相差 1%。高度不对称透镜的焦点特性可以通过跟踪穿过透镜的两条射线来获得,一条平行于轴进入,一条平行于轴离开。实际上,通过等效对称透镜追踪的单条光线可以很好地近似透镜的焦距。
实际透镜设计
图8中展示了 JEOL UHP 极片( $C_{s} \approx0.7 mm$ )的测量像差常数 $C_{s}$ 和 $C_{c}$ 的变化作为样品位置的函数。可以看到,存在一个能够最小化 $C_{c}$ 的最佳样品位置,但 $C_{s}$ 随着样品高度 $z_{o}$ 稳步降低。
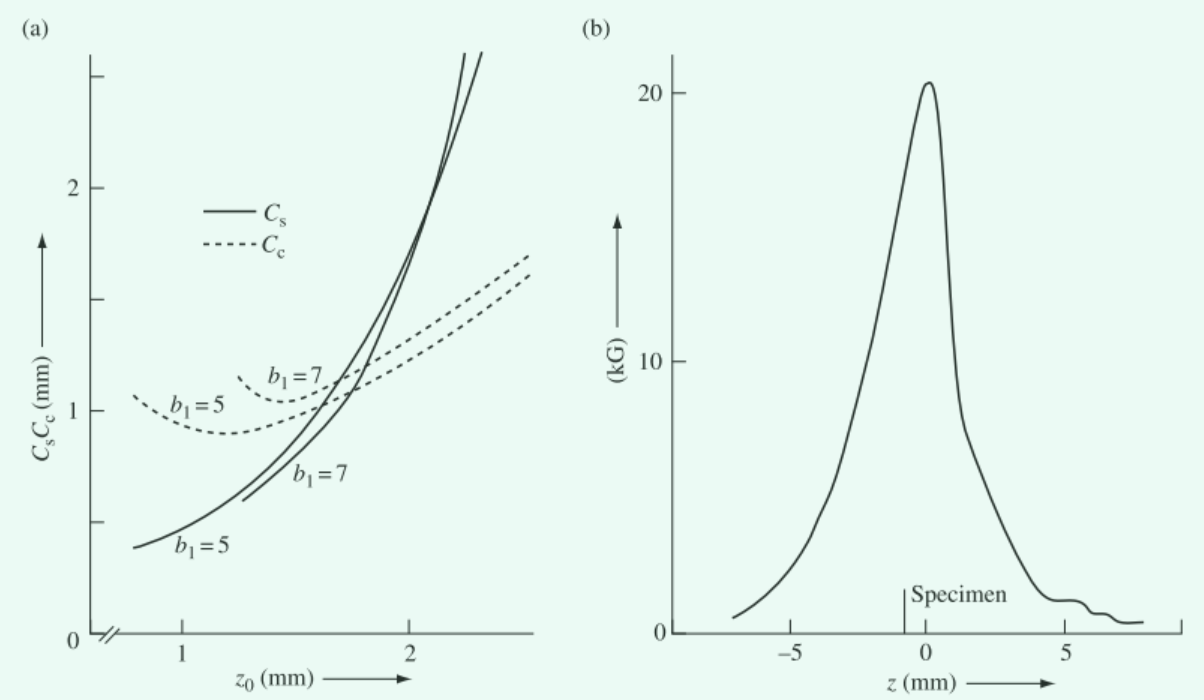
图8. (a) 对于JEOL UHP极片( $C_{s} \approx0.7 mm$ ), $C_{s}$ 和 $C_{c}$ 随样品位置的变化。在这里, $z_{o}$ (样品位置)是从下极片的顶部测量的。(b)通过图像旋转法获得的测量的透镜场分布。显示了样品的位置,即透镜的大部分屈光效应发生的位置。纵坐标表示轴向场强的 $z$ 分量,以千高斯(kilogauss)为单位。
这里 $b_{1}$ 是上部杆件直径(下部直径为 2 mm)。图8(b) 显示了透镜场分布,通过观察边缘沿光轴向下移动时的阴影图像旋转来测量。磁场的上限由极片铁的饱和来进行设定——对于 Permendur ,一种常用的铁类型,典型的饱和流密度(saturation flux density)为2.4 T(24 000 G)。从这些或者与之相类似的曲线中,我们发现球差和色差常数与透镜的焦距处于同一数量级,并且以类似方式随镜头激发而变化。最佳色差的最佳样品位置被发现在能够很好地靠近透镜中心的照明侧,而通过将样品放置在靠近透镜中心的位置可以最大限度地减少球面像差。通过 $eqn(3)$ , $eqn(*)$ , 及 $eqn(9)$ ,我们可以看到,透镜间隙的减少增加了间隙中的通量,并且减少了透镜的焦距,除非另有其他限制。显微镜的整体仪器放大可以增加通过减少投影透镜的透镜间隙,或者如果额外的散热可以通过透镜冷却系统进行吸收,也可以通过增加透镜的电流,从而使仪器更适合高分辨率工作。高倍率下非常大的焦深意味着可以通过减少投影透镜的焦距来增加整体放大倍率,而不会改变其他透镜的强度。