In the problem of logistic regression, MSE (Mean Squared Error) is not good enough to describe the loss of the training model. Cross entropy is an important concept in logistic regression, which comes from the information theory.
The amount of information
First of all, I will talk about the amount (quantity) of information (信息量), can be defined by $I$,
$$ I(x_0) = -\log(p(x_0))\tag{1} $$
in which, $x_0$ is a random event, and $p(x_0)$ will be the probability of $x_0$ event occurs.
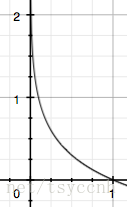
To describe the probability ( $p(x_0)$ ) which in the range of $[0,1]$.
It’s a very interesting thing, because when a small probability event occurs means a bigger amount of information.
Entropy
There is another concept named entropy ($H(X)$), which describes the mathematical expectation of all events’ ($x_i$) amount of information,
$$ H(X) = -\sum_{i=1}^n p(x_i)\log(p(x_i))\tag{2} $$
In the problem of binary classification,
$$
\begin{aligned}
H(X) &= -\sum_{i=1}^n p(x_i)\log(p(x_i))
&= -p(x)\log(p(x)) - (1 - p(x))\log(1-p(x))
\end{aligned}\tag{3}
$$
Relative entropy (Kullback-Leibler (KL) divergence)
$D_{KL}(P|Q)$ is often called the information gain achieved if P is used instead of Q.
$$ D_{KL}(p|q) = \sum_{i=1}^{n}p(x_i)\log\left(\frac{p(x_i)}{q(x_i)}\right)\tag{4} $$
from which, we can get the truth that, the smaller $D_{KL}$ is, the closer distribution q and distribution p will be.
Cross entropy
$(4)$ can be transformed into,
$$
\begin{aligned}
D_{KL}(p|q) & = \sum_{i=1}^{n}p(x_i)\log(p(x_i)) - \sum_{i=1}^{n}p(x_i)\log(q(x_i))
& = -H(p(x)) + H(p,q)
\end{aligned}\tag{5}
$$
where, the $H(p,q)$ is the so called cross entropy, we use the $H(p,q)$ to evaluate the loss of training model instead of the relative entropy $D_{KL}(p|q)$ , it is because the entropy ( $H(p)$ ) is remaining unchanged during the model training process.
In the problem of binary classification, $(5)$ will be transformed into,
$$
\begin{aligned}
H(p,q) & = -\sum_{i=1}^{n}p(x_i)\log(q(x_i))
& = -p(x)\log(q(x)) - (1-p(x))\log(1-q(x))
\end{aligned}\tag{6}
$$
If, we use $y$ to represent the real value while $\hat{y}$ to represent the trained value $(6)$ can be rewritten as,
$$ J = - y\log{\hat{y}} - (1-y)\log{(1-\hat{y})}\tag{7} $$