Back Propagation

给定一个神经网络，我们想通过Back Propagation的方法来求解图中任意节点的误差值（ $\delta$ ）。

图中，我将input unit定义为红色，并将output unit定义为绿色。这样很容易理解, input layer中只存在有 input unit，而输出层中也就只有绿色的 output unit。

我们假设有，

$$ \delta = \frac{J}{z} \tag{1} $$

其中 $J$ 为 cost function，而，$z$ 即为对应 unit 的输入input unit （同时也是上一层的output unit）。

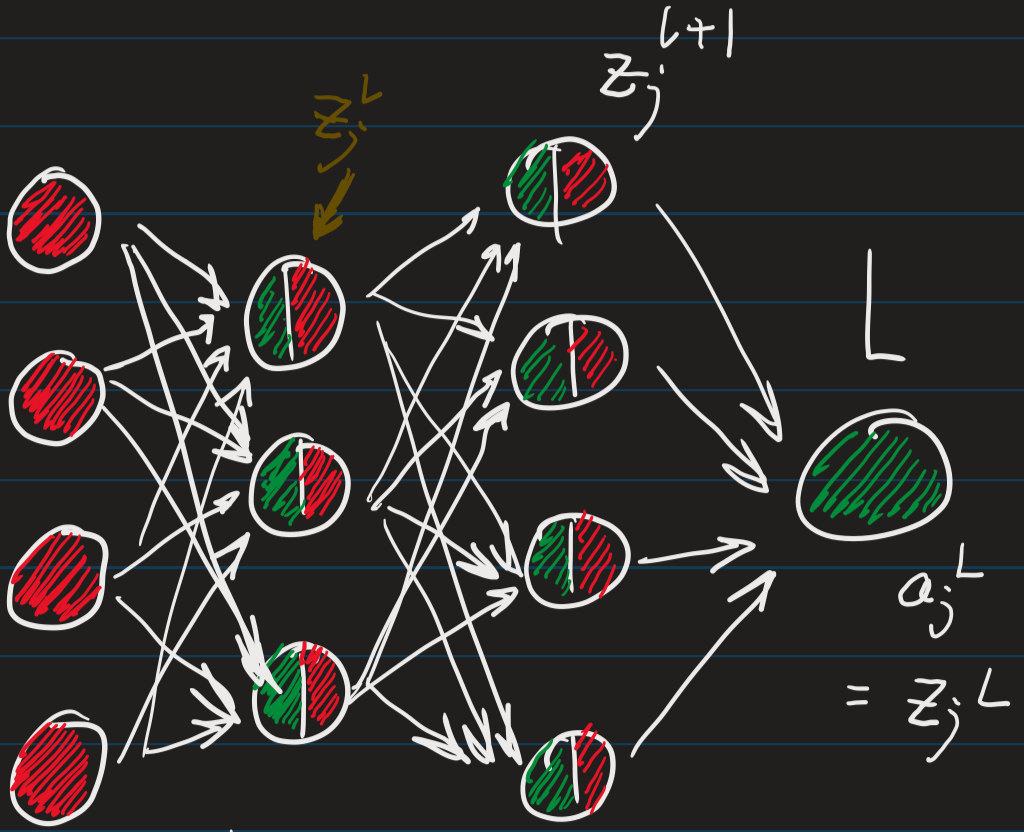
首先考虑 output layer (L层)，有如下关系式，

$$ a_j^{(L)} = z_j^{(L)} $$

即其 input unit == output unit。另外根据链式法则，有如下的求导关系：

$$L \rightarrow a_j^{(L)} \rightarrow z_j^{(L)}$$

所以有，

$$ \delta_j^{(L)} = \frac{\partial L}{\partial z_j^{(L)}} = \frac{\partial L}{\partial a_j^{(L)}}\cdot\frac{\partial a_j^{(L)}}{\partial z_j^{(L)}} = (a_j^{(L)} - y_j^{(L)})\cdot 1 $$

这样也能够解释为什么选用偏微分的形式来表示 $\delta$ ，即可以联系链式法则，为后续的反向传播做铺垫，在值上又与误差的定义相同，十分的精彩与美丽。

那么对于其中任意个 node 上的任意一个 unit 又如何来计算误差值呢？

例如以求解图中黄色的 $z_j^{(L)}$ 为例，同样由链式法则公式，首先观察链式的关系式。

$$ L \rightarrow z_k^{(l+1)}(k = 1,…, s_{(l)})\rightarrow z_j^{(l)} $$ 其中 $s_{(l)}$ 为 back propagation 中前一层中所有 input layer 中的 unit 数，所以由链式法则，有 $$ \delta_j^{(l)} = \sum_k^{s_{(l+1)}} \frac{\partial L}{\partial z_k^{(l+1)}}\cdot \frac{\partial z_k^{(l+1)}}{\partial z_j^{(l)}} = \sum_k^{s_{(l+1)}}\delta_k^{(l+1)}\cdot \frac{\partial z_k^{(l+1)}}{\partial z_j^{(l)}}\tag 2 $$

又因为由 forword propagation 可以得到，

$$ z_k^{(l+1)} = \sum_p^{s_{(l)}}\theta_{kp}^{(l)}\cdot g(z_j^{(l)}) + b_k^{(l)} \tag 3 $$

代入 $(2)$ 中，

$$ \delta_j^{(l)} = \sum_k^{s_{(l+1)}}\delta_k^{(l+1)}\cdot g^{‘}(z_j^{(l)}) = \sum_k^{s_{(l+1)}}\delta_k^{(l+1)}\cdot a_j^{(l)}\cdot(1-a_j^{(l)}) $$

再来观察关于 $J$ 和 $\theta_{ij}^{(l)}$ 的求导关系：

$$ L \rightarrow z_k^{(l+1)} (k = 1, …, s_{(l)}) \rightarrow \theta_{ij}^{(l)} $$

由链式法则，

$$ \frac{\partial L}{\theta_{ij}^{(l)}} = \sum_k^{s_{(l)}}\frac{\partial L}{\partial z_j^{(l+1)}}\cdot \frac{\partial z_k^{(l+1)}}{\partial \theta_{ij}^{(l)}}= \sum_k^{s_{(l)}} \delta_j^{(l+1)}\cdot \frac{\partial z_k^{(l+1)}}{\partial \theta_{ij}^{(l)}}

$$

当 $k = i, p = j$ 时，$(3)$ 代入原式求导可消去 $\sum$ 留下一项，

$$ \frac{\partial L}{\theta_{ij}^{(l)}} = \delta_j^{(l+1)}\cdot g(z_j^{(l)}) = \delta_j^{(l+1)}\cdot a_j^{(l)} $$