• § 1.1 实数
  • 1.1.1 数轴的建立
  • 1.1.2 建立数轴后引出的2个问题
• § 1.2 无尽小数
• § 1.3 收敛和收敛数列
  • 1.3.1 极限的数学定义
  • 1.3.2 几个结论及证明
• § 1.4 收敛数列的性质
  • 1.4.1 收敛数列极限的唯一性
  • 1.4.2 数列的有界性质
  • 1.4.3 子数列的性质
  • 1.4.4 极限的运算性质
  • 1.4.5 无穷小的性质
  • 1.4.6 夹逼定理
  • 1.4.7 通过不等式表达的收敛数列性质
• § 1.5 极限概念的推广

§ 1.1 实数

任何有理数 $r$ 都可以表示为两个整数之商：

$$r = \frac{p}{q}$$

1.1.1 数轴的建立

其中 $p,q\in Z$ 且$q\neq 0$。根据以上定义首先建立数轴:

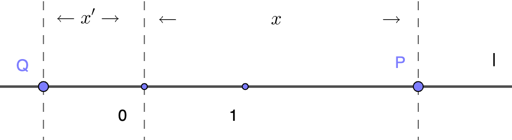
建立坐标轴后，就可以建立平面和空间坐标系，从而建立解析几何学。

1.1.2 建立数轴后引出的2个问题

问题1. 数轴上每一个点对应一个实数为其坐标，那么每一个实数是否都是数轴上某一点坐标呢？

• 对固定的正整数 $q$，让 $p$ 取遍所有整数，则 $p/q$ 这些数字把数轴分成了长度为 $1/q$ 的区间。

• 令每一个实数 $x$ 位于这些中的一个区间，也就是说对任意固定的实数 $x$ 一定可以找出一个整数 $p$ ，使得，

$$\frac{p}{q} \leq x<\frac{p+1}{q} \qquad (1)$$

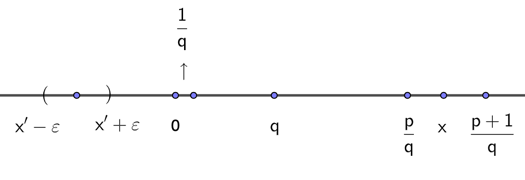
由 (1) 可得，

$$ |x-\frac{p}{q}|<\frac{1}{q} $$

即，$\forall x$ ，总能找到一个有理数 $p/q$ 和$x$的距离可以小于 $1/q$ 。

如一个新的实数点 $x’$，要证明 $x-\varepsilon$ 与 $x+\varepsilon$ 之间有无穷多个数，则

故有，

$$ \left|x-\frac{p}{q}\right|<\varepsilon $$

即找到了一个有理数 $p/q$ 确实落在 $\varepsilon$ 的区间内部。

根据这个问题，我们得到两个结论：

1. 有理数在数轴上是稠密的
   
   • 即随便取一个实数，在充分小的区间就能找到无穷多有理数。
   • 同样的，在充分小的区间内有一个有理数，也就相当于有无穷多个有理数。
2. 任何实数，都可以由无理数来任意逼近

问题2. 有理数是连续的吗？即无理数的引出

例：

若 $n$不是平方数，那么 $\sqrt{n}$ 不是有理数。

证明：假定

$$ \sqrt{n}=\frac{p}{q} $$ 就有， $$ n=\frac{p^{2}}{q^{2}} \quad, \quad p^{2}=n q^{2} \qquad (2) $$

其中，$p$ 和 $q$ 的定义同 问题1。

由 $p/q$ 一定不是整数得到，

$$ m<\frac{p}{q}<m+1 \quad\left(m \in N^{*}\right) \quad \rightarrow \quad mq<p<m q+q $$

即，

$$ 0<p-m q<q $$

由 (2) 得，

$$ p^{2}-p m q=n q^{2}-p m q $$

$$ p(p-m q)=q(n q-p m) \rightarrow \frac{p}{q}=\frac{n q-p m}{p-m q} \quad (3) $$

令 (3) 等于 $p_1/q_1$，由

$$ p-m q>0 \rightarrow q_{1}>0 \rightarrow 0<q_{1}<q $$

$$ p_{1}=\frac{q_{1}}{q} \times p<p $$

推出以下关系式，

$$ \sqrt{n}=\frac{p}{q}=\frac{n q-p m}{p-m q}=\frac{p_{1}}{q_{1}}=\frac{p_{2}}{q_{2}}= \cdots \quad (4) $$

但由于 $p$ 与 $q$ 均为正整数，所以不可能无限制 (4) 中的关系，所以假设不成立，所以 $\sqrt{n}$ 不是有理数。

§ 1.2 无尽小数

任何一个有理数是有穷小数或者无穷循环小数，我们可以从以下实例中得到证明。

$$ \begin{array}{l} a=1.\dot{2}3\dot{4} =1+0.\dot{2}3 \dot{4}=1+b

b=0 . \dot{2}3\dot{4}

10^{3} b=234. \dot{2}3\dot{4}=234+b

(10^3-1) b=234, \quad b=\frac{234}{999}=\frac{26}{111}

\rightarrow a=1+\frac{26}{111}=\frac{137}{111} \end{array} $$

实际上，实数都可以表示为无尽小数。

$$ n. a_{1} a_{2} a_{3}… $$

而实数本身可以分为有理数 (循环小数) 及无理数 (不循环小数)。

数轴上的任何一个点一定对应着一个实数，但大多数在数轴上是对不准的。

这里就引入另外一个定理，区间套定理，如对于点，

$$ a=n.a_{1} a_{2} a_{3} $$

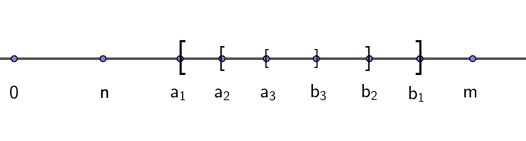
$ \left[a_{1}, a_{2}\right] > \left[a_{1}, b_{2}\right]>\left[a_{3}, b_{3}\right]>\ldots $ 不断循环嵌套下去，存在唯一一个点与之对应。

即实数与数轴上的点是一一对应的。

§ 1.3 收敛和收敛数列

当 $n$ 很大时，$a_{n}$ 无限接近，即

$$ a_{n} \rightarrow a \Rightarrow n \rightarrow \infty时 \lim {i \rightarrow \infty} a{n}=a $$

用一个数轴来描述a的 $\varepsilon$ 邻域，

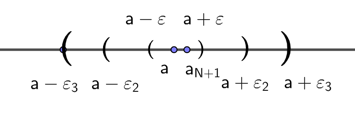
对 $\forall \varepsilon > 0$，$\exists N \in N^{*}$ 当 $n > N$ 时，

$$ a-\varepsilon<a_{n}<a+\varepsilon $$

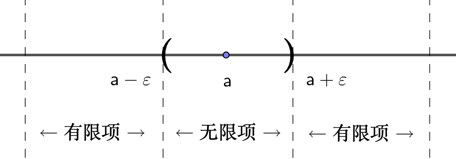
当 $n>N$ 时，

$$ a_{1} a_{2} … a_{N}(有限项)|a_{N+1}…(无限项) $$

1.3.1 极限的数学定义

$$ \left|a_{n}-a\right|<\varepsilon \Rightarrow a-\varepsilon<a<a+\varepsilon $$

1.3.2 几个结论及证明

结论一

$$ |q|<1, \quad \lim _{n \rightarrow \infty} q^{n}=0 $$

证明：

• 方法 1

  • $q=0$ 时，显然成立
  • $q \neq 0$ 时，

$$ \begin{array}{c} \alpha=\frac{1}{|q|}-1>0, \quad \frac{1}{|q|}=1+\alpha, \quad|q|=\frac{1}{1+\alpha}

\forall \varepsilon>0, \quad \exists N \in N^{*}, \quad n>N \quad\left|q^{n}\right|<\varepsilon

\left|q^{n}\right|=|q|^{n}=\frac{1}{(1+\alpha)^{n}}=\frac{1}{1+n \alpha+\cdots \cdots \alpha^{n}}<\frac{1}{n a}<\varepsilon

n>\frac{1}{\alpha \varepsilon} \quad, \quad N=\left[\frac{1}{\alpha \varepsilon}\right] \end{array} $$

• 方法 2

$$ |q|^{n}<\varepsilon, \quad n \cdot \log |q|<\log \varepsilon, \quad n>\frac{\log \varepsilon}{\log |q|}, \quad N=\left[\frac{\log \varepsilon}{\log |q|}\right] $$

结论二

$$ \lim _{n \rightarrow \infty} \sqrt[n]{n}=1 $$

证明：

$$ \forall \varepsilon>0, \quad \exists N, \quad n>N 时, \quad |^{n}\sqrt{n}-1 |<\varepsilon $$

$$ ^n\sqrt{n} = ^n\sqrt{11…1\bigl((n-2)个1\bigr)\sqrt{n}} <\frac{n-2+2 \sqrt{n}}{n}=\frac{n+2(\sqrt{n}-1)}{n}=1+\frac{2(\sqrt{n}-1)}{n} $$

$$ 0 \leqslant {^n\sqrt{n}}-1<\frac{2(\sqrt{n}-1)}{n}=\frac{2(\sqrt{n}-1)}{\sqrt{n} \cdot \sqrt{n}}<\frac{2}{\sqrt{n}} \Rightarrow n>\frac{4}{\varepsilon^{2}} $$

$$ N=\left[\frac{4}{\varepsilon^{2}}\right] $$

总结

$\lim_{n \to \infty} a_{n}=a$的描述方法

$$ \forall \varepsilon>0 \quad \exists N \in N^{*}, \quad \forall n>N，有 \quad\left|a_{n}-a\right|<\varepsilon $$

$\lim_{n \rightarrow \infty} a_{n} \neq a$的描述方法

$$ \exists \varepsilon_0 > 0, \quad 不论 \quad N^* 多大，总是 \exists n > N，有\quad |a_n-a|\geqslant \varepsilon_0 $$

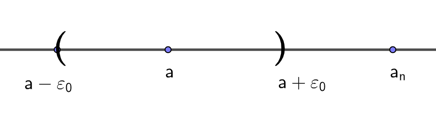
§ 1.4 收敛数列的性质

收敛 $\rightarrow$ 有极限

不收敛 $\rightarrow$ 发散

用数轴来描述 $lim_{n\rightarrow\infty}a_n = a$, 如图：

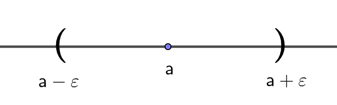
下面来介绍收敛数列的几个重要的性质。

1.4.1 收敛数列极限的唯一性

• 收敛数列极限是唯一的。

对于这个定理，我们可以首先从数轴上考虑, 如下图所示：

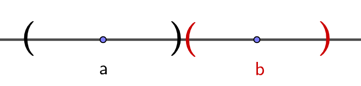
由于b区间内存在有限项，但在a中是无限多项，所以矛盾。

证明如下：

$$ \lim {n \rightarrow \infty} a{n}=a, \quad \lim {n \rightarrow \infty} a{n}=b \quad \Rightarrow \quad a=b $$

$$ \begin{array}{l} \forall \varepsilon>0, \quad N_{1}, \quad n>N_{1} \quad\left|a_{1}-a\right|<\frac{\varepsilon}{2}

\forall \varepsilon>0, \quad N_{2}, \quad n>N_{2} \quad\left|a_{1}-b\right|<\frac{\varepsilon}{2} \end{array} $$

$$ 取\quad N=\max \left(N_{1}, N_{2}\right), n>N\quad时 $$

$$ \begin{array}{c} |a-b|=\left|a-a_{n}+a_{n}-b\right| \leq\left|a-a_{n}\right|+\left|a_{n}-b\right|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon

\Rightarrow a=b \end{array} $$

1.4.2 数列的有界性质

首先引出有界的概念：

• $a_n \leq B \Rightarrow$ 有上界
• $a_n \geq A \Rightarrow$ 有下界
• $A \leq a_n \leq B \Rightarrow$ 有界
  • $\left|a_n\right|\leq M$

下面为定理1.4.2：

• 数列一定是有界的。

数轴上描述如下，

证明如下，

$$ \lim_{n \rightarrow \infty}a_n = a $$

$$ \begin{array}{c} \varepsilon = 1，\exists N，n>N时，\left|a_n-a\right|<1

\left|a_n\right|\leq\left|a\right|+1，n>N

取\quad M = |a_1|+|a_2|+…+|a_N|+|a|+1\quad (|a_1|+…+|a_N|代表外面的有限项)

即\quad |a_n|<M，n=1, 2, 3…

\end{array} $$

1.4.3 子数列的性质

对于一个数列，如下，

$$ a_1，a_2，a_3，…，a_n，… $$

从中选取无穷项称为原来数列的子数列 (不能改变顺序)，如下，

$$ a_{k1}，a_{k2}，a_{k3}，a_{k4}，…\quad \Rightarrow \quad k_n \geq n $$

定理 1.4.3 如下:

• 设$lim_{n\to\infty}a_n=a$，那么${a_n}$的任何子数列必以 $a$ 为极限。

证明如下：

$$ \begin{array}{c} \lim_{n\to\infty}a_n=a，a_{kn}=b_n

\varepsilon > 0，\forall\varepsilon > 0，\exists N，当n>N，\left|a_n-a\right|<\varepsilon

n>N时，\left|b_n-a\right| = \left|a_{kn}-a\right|

由 k_n \geq n > N，\left|b_n-a\right|=\left|a_{kn}-a\right|<\varepsilon

\end{array} $$

定理 1.4.3 有两个应用：

• 根据子数列不收敛来判断原数列不收敛

  例 判断 ${(-1)^{n-1}}$ $(1，-1，1，-1，…)$ 的收敛性质。

    即通过 (1，1，1，...) 以及 (-1，-1，...) 两个数列收敛的极限不同。
  

• 判断周期函数是否收敛

  例 判断 $a_n=\sin{n}$ 数列是否收敛。

  证明：找一个子数列 {$\sin{k_n}$}

$$ k_n\in(n \pi + \frac{\pi}{3}，n \pi + \frac{2\pi}{3})，长度为\frac{\pi}{3} > 1 $$

如果一个区间比1大，则这个区间中至少有一个正整数。

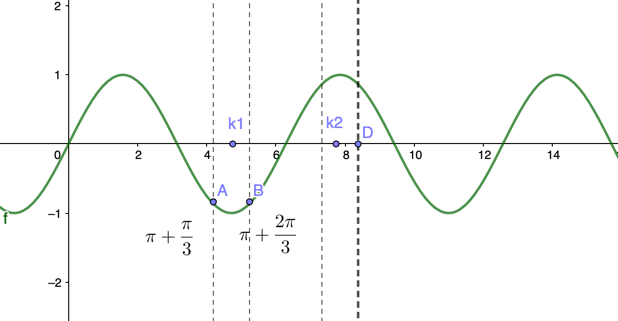
$$ k_1 \in (\pi+\frac{\pi}{3}，π+\frac{2\pi}{3}) ，k_2 \in (2\pi+\frac{\pi}{3}，2\pi+\frac{2\pi}{3}) $$

则有，

$$ \begin{array}{c} \sin{k_1} < \sin{\pi+\frac{\pi}{3}} = - \frac{\sqrt{3}}{2}

\sin{k_2} > \sin{2\pi+\frac{\pi}{3}}= \frac{\sqrt{3}}{2}

\end{array} $$

所以，两个子数列收敛到了不同的极限，所以$\sin{n}$不收敛。

1.4.4 极限的运算性质

• 设 ${a_n}$，${b_n}$是两个收敛数列，则

  1. $\lim(a_n \cdot b_n)=\lim(a_n) \pm \lim(b_n)$
  2. $\lim(a_n \cdot b_n)=\lim(a_n) \cdot \lim(b_n)$
  3. $若\lim(b_n) \neq 0，则 \lim{\frac{a_n}{b_n}}=\frac{\lim(a_n)}{\lim(b_n)}$

• 证明 1：$\lim{a_n}=a, \lim{b_n}=b \Rightarrow \lim{(a_n \pm b_n)}=a \pm b$

$$ \begin{array}{c} \forall \varepsilon >0，\exists N，n>N时，|(a_n+b_n)-(a+b)| < \varepsilon

\forall \varepsilon >0，\exists N_1，n>N_1时，|a_n-a|<\frac{\varepsilon}{2} \quad (1)

\forall \varepsilon >0，\exists N_2，n>N_2时，|b_n-b|<\frac{\varepsilon}{2} \quad (2)

N = max(N_1，N_2)，当n>N时，(1)(2)均成立

|(a_n+b_n)-(a+b)| \leq |a_n-a|+|b_n-b| < \frac{\varepsilon}{2} + \frac{\varepsilon}{2}=\varepsilon
\end{array} $$

• 证明 2：$\lim{a_n}=a，\lim{b_n}=b \Rightarrow \lim{a_n\cdot b_n}=ab$

$$ \begin{array}{c} \forall \varepsilon >0 \exists N，n > N时，|a_nb_n - ab|< \varepsilon

|a_nb_n - ab|=|a_nb_n-ab_n+ab_n-ab|\leq|a_nb_n-ab_n|+|ab_n-ab|=|b_n||a_n- a|+|a||b_n-b| \quad (1)

假定 |b_n|\leq M，n=1，2…

\varepsilon > 0，\exists N_1，n>N_1时，|b_n-b|<\frac{1}{|a|+1}\cdot \frac{\varepsilon}{2}

\varepsilon > 0，\exists N_2，n>N_2时，|a_n-a|<\frac{\varepsilon}{2M}

当n>N=max(N_1，N_2)时，

(1)式 \Rightarrow |b_n||a_n-a|+|a||b_n-b|\leq M\cdot \frac{\varepsilon}{2M} + |a|\cdot \frac{1}{|a|+1}\cdot \frac{\varepsilon}{2}< \varepsilon
\end{array} $$

• 证明 3：$\lim\frac{1}{b_n} = \frac{1}{b}$

$$ \begin{array}{c} \forall \varepsilon >0，\exists N，当n>N时，|\frac{1}{b_n}-\frac{1}{b}|<\varepsilon

\forall \varepsilon > 0，\exists N_1，n > N_1时，|b_n-b|< \frac{|b|}{2} \Rightarrow |b_n| > \frac{|b|}{2} > 0

又令 |b - b_n|< \frac{|b|^2}{2} \cdot \varepsilon

\Rightarrow |\frac{1}{b_n} - \frac{1}{b}|=\frac{|b-b_n|}{b\cdot b_n} < \frac{2|b-b_n|}{|b|\cdot \frac{|b|}{2}} = \frac{2|b-b_n|}{|b|^2}< \frac{2}{|b|^2}\cdot \frac{|b|^2}{2}\cdot \varepsilon = \varepsilon
\end{array} $$

1.4.5 无穷小的性质

首先引入无穷小量 (无穷小数列) 的概念:

• 若 $\lim_{n\to \infty}a_n = 0$，则称 {$a_n$} 是无穷小量或称为无穷小数列。

下面为定理 1.4.5：

1. {$a_n$} 是无穷小 $\Rightarrow$ { $|a_n|$ } 是无穷小
2. {$a_n$}，{$b_n$}是无穷小，则{$a_n\pm b_n$}
3. 若{$c_n$}是有界数列，{$a_n$}是无穷小，则{$c_n\cdot a_n$}是无穷小
   • 注意: 如$a_n=\frac{1}{n}，b_n=\frac{1}{n^2}$，由于$\frac{a_n}{b_n}=\frac{1}{n} / \frac{1}{n^2} = n$，所以两个无穷小的商可能发散。
4. 若 $0\leq a_n\leq b_n$，则当{$bn$}是无穷小量时，{$a_n$}也是无穷小
5. $\lim_{n\to\infty}a_n = a \Rightarrow$ {$a_n-a$}是无穷小量

例：

若 $\lim_{n\to\infty}a_n=a，则 \lim\frac{a_1+…a_n}{n} = a$

证明如下：

$$ \begin{array}{c} 设 a=0，\lim_{n\to\infty}a_n=0 \Rightarrow \lim\frac{a_1+…+a_n}{n}=0

\forall \varepsilon > 0，\exists N，n> N时，|\frac{a_1+…+a_n}{n}|<\varepsilon

\forall \varepsilon > 0，\exists N，n> N时，a_n< \frac{\varepsilon}{2} \quad (1) \quad 由 (1)得，

|\frac{a_1+…+a_n}{n}|=|\frac{a_1+…+a_N+a_{N+1}+…+a_n}{n}|\leq \frac{|a_1+…+a_N}{n} + \frac{|a_{N+1}+…+a_n|}{n}\leq \frac{M}{n} + \frac{n-N}{n}\cdot \frac{\varepsilon}{2}< \frac{M}{n}+ \frac{\varepsilon}{2}

即n>N_1>max(N，[\frac{2M}{\varepsilon}])时，(\frac{M}{n}< \frac{\varepsilon}{2}，n > \frac{2M}{\varepsilon})

当a \neq 0，令b_n = a_n -a \rightarrow 0

\lim_{n\to\infty}{\frac{b_1+…+b_n}{n}}=\lim{\frac{(a_1-a)+…+(a_n-a)}{n}}=\lim(\frac{a_1+…+a_n}{n}-a)=0

\Rightarrow \lim{\frac{a_1+…+a_n}{n}}=a
\end{array} $$

1.4.6 夹逼定理

• $若a_n\leq b_n\leq c_n，n \in N^* 且\lim_{n\to\infty}a_n=\lim_{n\to\infty}c_n=a，则 \lim_{n\to\infty} b_n = a$

注：$a_n< b_n< c_n$ 时同样成立。

证明如下：

$$ \begin{array}{c} 0 \leq b_n-a_n \leq c_n-a_n

由 \lim{a_n}=\lim{c_n}

\Rightarrow 0\leq b_n-a_n\leq c_n-a_n \Rightarrow \lim_{n\to\infty}{(b_n-a_n)}=0

\lim_{b\to\infty}{b_n} = \lim{(b_n - a_n + a_n)} = \lim{a_n} \rightarrow a (n \rightarrow \infty)
\end{array} $$

例：

证明 $a>1，k \in Z^+$ 时，$lim_{n\to\infty}{\frac{n^k}{a^n}}=0$

证明如下：

$$ \begin{array}{c}
当k=1时，令a=1+\alpha，有

0<\frac{n}{a^n}=\frac{n}{(1+\alpha)^n}=\frac{n}{1+n\alpha+\frac{n(n-1)}{2}\cdot\alpha^2+…+\alpha^n}<\frac{n}{\frac{1}{2}\cdot n\cdot (n-1)\cdot \alpha^2}=\frac{2}{(n-1)\cdot \alpha}

\Rightarrow 0<\frac{n}{a^n}<\frac{2}{(n-1)\cdot \alpha}

由夹逼定理得，lim{\frac{n}{a^n}}=0

当k\neq 1时，

\lim\frac{n^k}{a^n}=\lim(\frac{n}{(a^{\frac{1}{k}})^n})^k=\lim(\frac{n}{b^n})^k= 0
\end{array} $$

例：

$\forall a>0，证明\lim_{n\to\infty}{^n\sqrt{a}}=1$

证明如下：

首先证明 $\lim{^n\sqrt{n}}=1$

$$ \begin{array}{c} \lim_{n\to\infty}(1\cdot 1\cdot 1\cdot …\sqrt{n}\cdot \sqrt{n})^{\frac{1}{n}}\leq \frac{n-2+2\sqrt{n}}{n}=1+ \frac{2(\sqrt{n}-1)}{n}

\Rightarrow 0\leq n^{\frac{1}{n}}-1 <\frac{2}{\sqrt{n}}

\forall \varepsilon > 0，取N=[\frac{4}{\varepsilon ^2}]

当n>N时，有|n^{\frac{1}{n}}-1|<\frac{2}{\sqrt{n}}<\varepsilon

\Rightarrow \lim_{n\to\infty}{^n\sqrt{n}}=1

当a> 1时，1< ^n\sqrt{a}< ^n\sqrt{n}，n> a

\Rightarrow \lim{1}< \lim{^n\sqrt{a}< \lim{^n\sqrt{n}}}

由夹逼定理得，\lim{^n\sqrt{n}}=1

当0< a< 1时，^n\sqrt{a}=\frac{1}{^n\sqrt{\frac{1}{a}}}，(n\to\infty)

令b=\frac{1}{a}

\Rightarrow \lim{^n\sqrt{a}} = \lim{\frac{1}{^n\sqrt{b}}}
\end{array} $$

例:

求 $\lim_{n\to\infty}(n^2-n+2)^{\frac{1}{n}}$

$$ \begin{array}{c} n^2-n+2=n^2-(n-2)< n^2，n> 2时成立

n>2时，有 n^2> 2(n-1)=2n-2，即 n^2-n+2> n

\Rightarrow n< n^2-n+2=n^2-(n-2)< n^2

\Rightarrow (n)^{\frac{1}{n}}< (n^2-n+2)^{\frac{1}{n}}< (n^2)^{\frac{1}{n}}

\lim{^n\sqrt{n}}=\lim(^n\sqrt{n}\cdot ^n\sqrt{n})= \lim(n^2)^{\frac{1}{n}}=1

\Rightarrow \lim(n^2-n+2)^{\frac{1}{n}}=1
\end{array} $$

例：

证明 $\lim_{n\to\infty}(\frac{1}{\sqrt{n^2+1}}+ \frac{1}{\sqrt{n^2+2}}+ …+ \frac{1}{\sqrt{n^2+n}})=0$

注意，不能应用极限的运算性质解决无限项的问题

证明如下：

$$ \begin{array}{c} a_n = \frac{1}{\sqrt{n^2+1}}+ \frac{1}{\sqrt{n^2+2}}+ …+ \frac{1}{\sqrt{n^2+n}}

a_1 = \frac{1}{\sqrt{1+1}}，a_2= \frac{1}{\sqrt{5}} + \frac{1}{\sqrt{6}}，a_3 = …

\frac{n}{\sqrt{n^2+n}} \leq 原式 \leq \frac{n}{\sqrt{n^2+1}}

\lim{n}{\sqrt{n^2+n}}=\lim{\frac{1}{\sqrt{1+\frac{1}{n}}}}=1=\lim\frac{n}{n^2+1}=\lim\frac{1}{1+\frac{1}{n^2}}
\end{array} $$

1.4.7 通过不等式表达的收敛数列性质

• $\lim_{a\to\infty}{a_n=a}，\alpha < a < \beta，\exists N，当n> N时有，$

$$ \alpha < a_n < \beta $$

• $\lim_{n\to\infty}{a_n=a}，\lim_{n\to\infty}{b_n=b}，若a< b，则n > N时有，$

$$ a_n < b_n $$

• $\lim_{n\to\infty}{a_n=a}，\lim_{n\to\infty}{b_n=b}，如果n> N时，a_n \leq b_n时，则有，$

$$ a \leq b $$

$\qquad 证：若a>b，与n> N时，a_n \leq b_n矛盾$

§ 1.5 极限概念的推广

• $\lim_{n\to\infty}a_n = +\infty$

  定义：对$\forall A>0，\exists N，当n> N时，有a_n > A$

• $\lim_{n\to\infty}a_n = -\infty$

  定义：对$\forall A>0，\exists N，当n> N时，有a_n <-A$

• $\lim_{n\to\infty}a_n = \infty$

  定义：对$\forall A>0，\exists N，当n> N时，有|a_n|>A$

如 {$(-1)^n\cdot n$} 这个数列，可以是围绕A点左右跳跃的，如上图所示。