In TEM, there are two kinds of contrast:
Amplitude Contrast
As you can see in the figure,
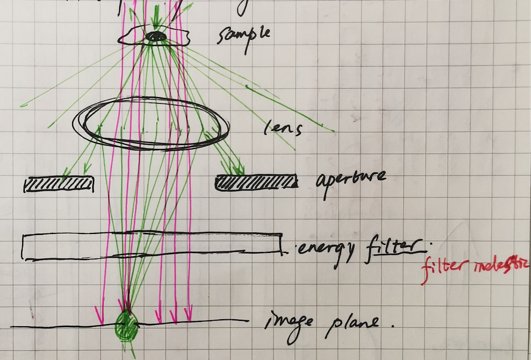
When the incident electrons ‘light’ on the sample, there will be three kinds of resulted electrons, which is also mentioned before in the ‘The interaction between the electron and the sample’, they are unscattered primary electrons, inelastically scattered primary electrons and elastically scattered primary respectively.
For the unscattered primary electrons (in pink), they are not influenced by the sample and no energy or amplitude (intensity) is changed.
For the inelastically primary electrons (not given in the figure), which has lost part of energy transfered by interaction with the sample, which can be filtered out by the inelastically primary electrons. So basecally, we don’t need to discuss the inelastically primary.
For the elastically (in green), it will be interesting, because as mentioned before, although there will be no energy transfer during interaction with the sample (which means they will not filtered out by eneryg filter), some electrons will scattered with a very high angles or even returning from the original road, which will do no contribution to the image. So, there will be the aperture to limit the elastically scattered electrons into some fixed angle range. The result is, the amplitude of the scattered electrons will decrease and make the fisrt contrast with the unscattered electrons. It is the so-called amplitude contrast.
Phase contrast
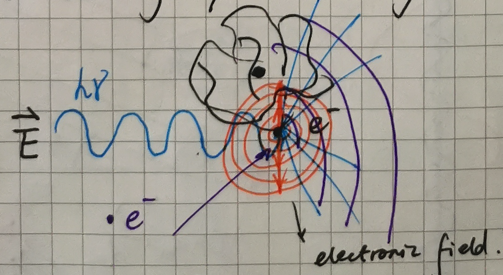
Like double slit experiment, an electron microscope is like a billion slit experiment each electron idividually feels all the atoms of the sample and collecting all of their scattering to produce an image.
When the incident electrons interact with the electrons in the track of the sample atoms, electrons will go along any directions and angles which will create the wave as seen in the figure,
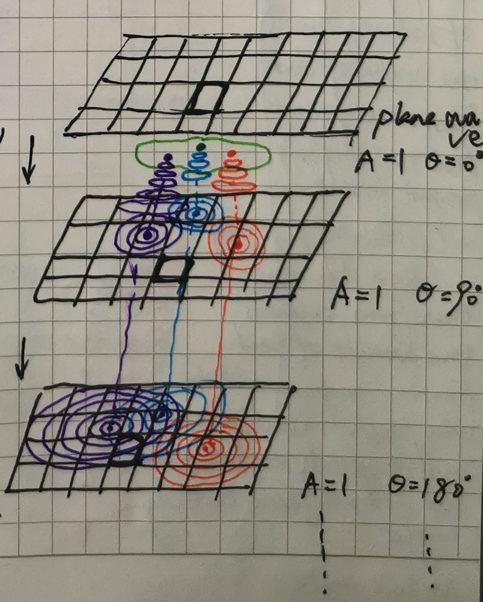
After which, many plane waves derived from the interactions between incident electrons and the atoms electrons will pass through the imaginary plane with different phase angle (Θ),
In this way, the create a very complex phase riples situations, different interactions make different plane waves with different spreading angles,
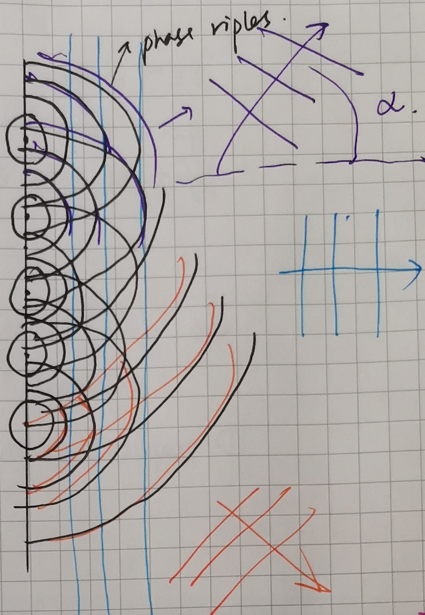
This angle, we call it ‘α’. First of all, let’s think of it in a more complex view step by step,
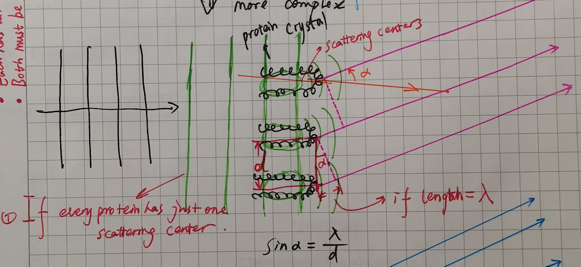
Before discussing, there is a very important equations in crystallography, braggs equation:
$$sinα = λ/d$$
, where α is the incident angle, λ is the wave length and d is the spacing of the crystal faces formed by the repeating unit.
We think of the repeating unit as every integrate protein structures, in other words, think of the every whole proteins as the scattering centers. Referenced by the braggs equation, gives a α, we name it $α_1$.
Let’s go on, in the next figure, I showed a more complex situation, when the scattering center is more and more ‘detailed’, will gives a bigger and bigger ‘α’, and
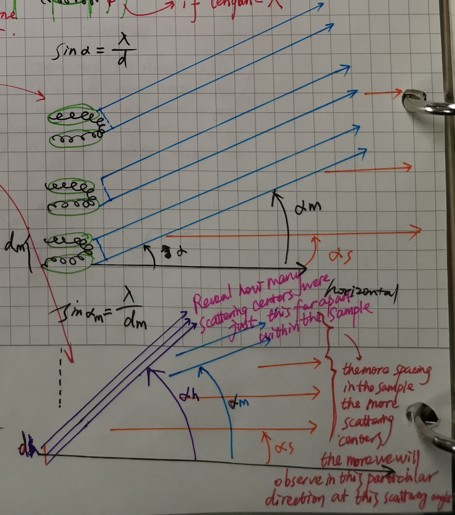
$ α_1 < α_2 < … <α_n $
From this example, we can also get a conclusion, the higher angle of the incident angle, the higher resolution of the structural information we will get. As seen in the figure bellow,
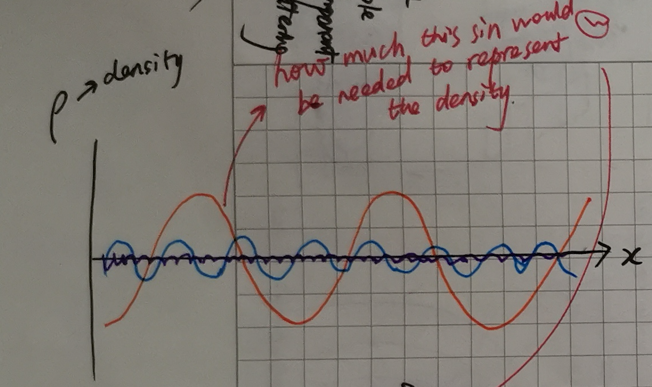
which Y-axis shows the density and showing how much this sin function would be needed to represent the density.
In the end, let’s discuss something in crystallography. Because cryo-EM is very similar to the crystallography. The figure bellow gives a diffraction image model,
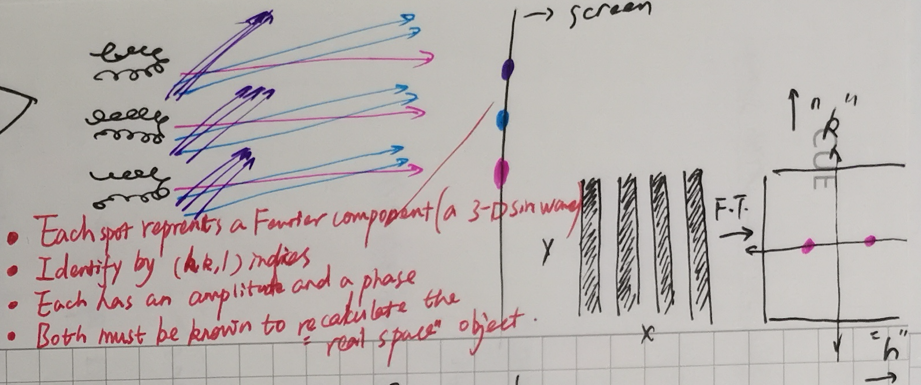
Where does the diffraction point come from?
- Each spot represents a Fourier component (a 3-D sin wave)
- Identify by miller index (h, k, l)
- Each has an amplitude and a phase
- Both must be known to recalculate the “real space” object