The related information of correlation is mostly from David Dorran video at youtube, it is very clear and easy understanding.

What Is Correlation

Correlation is a measure of how similar signals are. They are present in things like discrete Fourier transform.

Which is always present as equation:

Eq. (1)

$$Corr_{x,y} = \sum_{n=0}^{N-1}x[n]\cdot y[n]$$

Where $x[n]$ and $y[n]$ are two discrte function.

Here gives an example,

$x=$ $$\begin{bmatrix}1&3&-2&4\\end{bmatrix}$$

$y=$ $$\begin{bmatrix}2&3&-1&3\\end{bmatrix}$$

$z=$ $$\begin{bmatrix}2&-1&4&-2\\end{bmatrix}$$

plot them in matlab, we get this

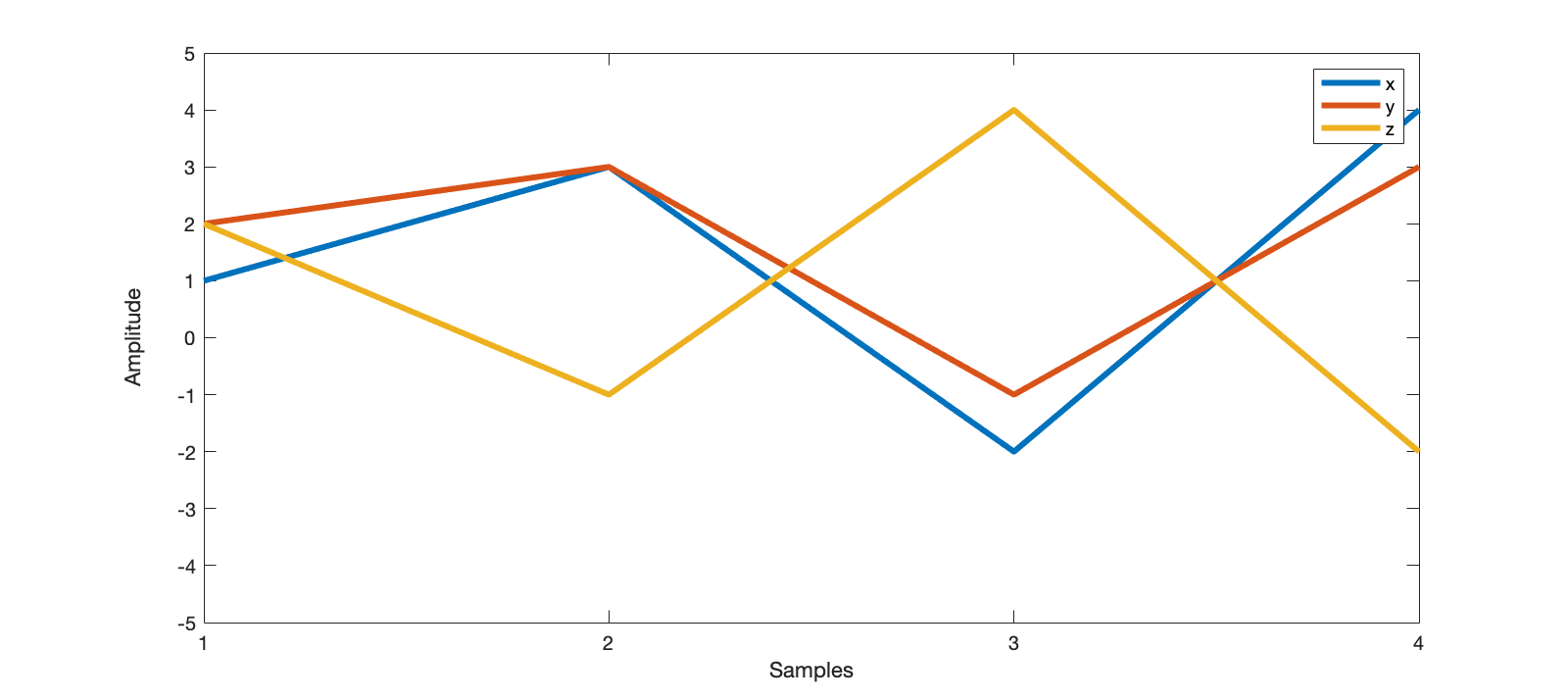
From this figure we can find x is similar with y but not similar with z. How we can describe this in mathematics?

We substitute x, y and y, z into Eq. (1),

$$ \begin{aligned} \operatorname{Corr}_{x, y} &=x[0] y[0]+x[1] y[1]+x[2] y[2]+x[3] y[3] \\ &=(1)(2)+(3)(3)+(-2)(-1)+(4)(3) \\ &=2+9+2+12=25 \end{aligned} $$

and

$$ \begin{aligned} \operatorname{Corr}_{y,z} &= y[0]z[0] + y[1]z[1] + y[2]z[2] + y[3]z[3] \\ &= (2)(2)+(3)(-1)+(-1)(4)+(3)(-2) \\ &= -9 \end{aligned} $$

However if we substitute the first 2 in Z into 100, which will lead to $Corr_{y,z} = 187$, and we will become confused, because we can’t get clearly which two are more similar with the other. as seen in the figure:

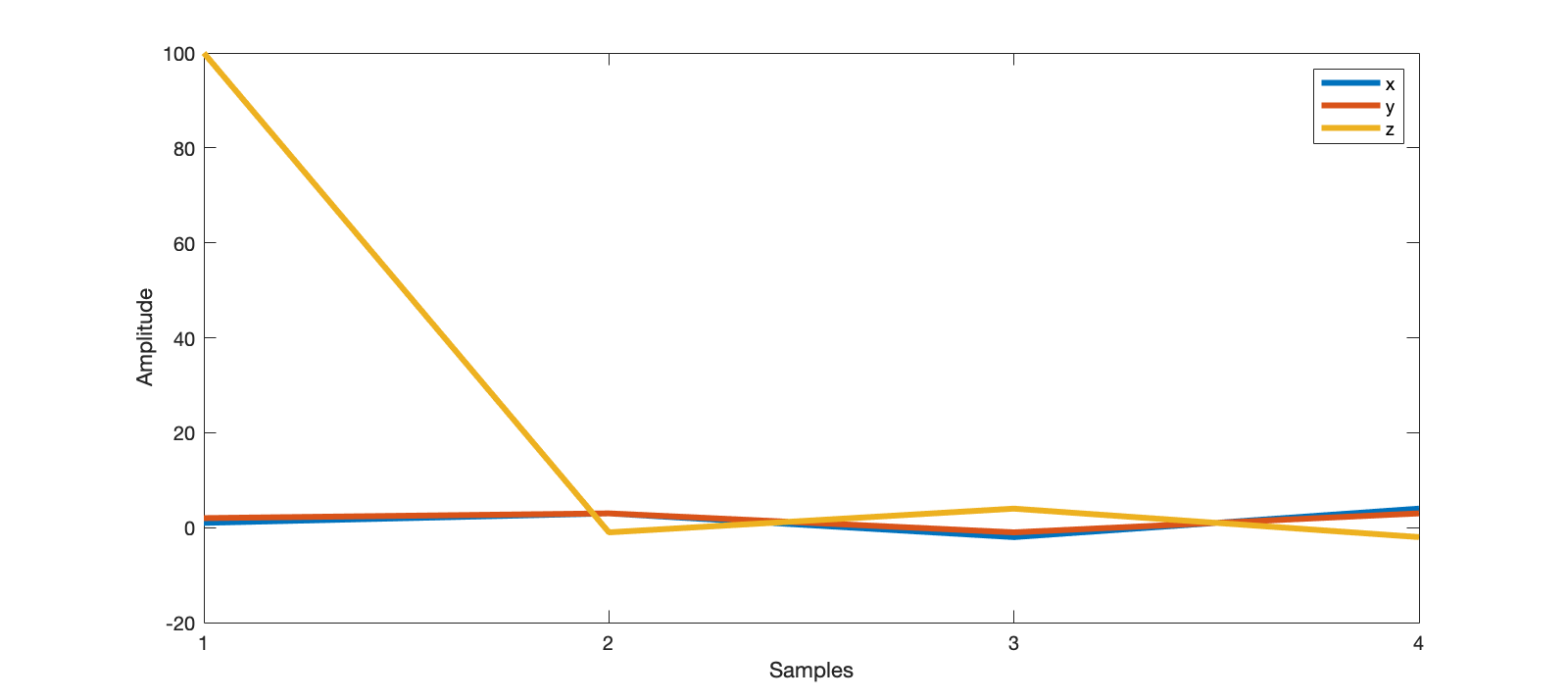
So here we need Normalised Correlation.

$$ \operatorname{Corr}{norm{x,y}}=\frac{\sum_{n=0}^{N-1} x[n]y[n]}{\sqrt{\sum_{n=0}^{N-1} x^{2}[n] \sum_{n=0}^{N-1} y^{2}[n]}} $$

The two terms at denominator are the measure of energy in signal X and Y respectively, which make the denominator the overall scaling factor.

Basically, this normalised correlation function is this result divided by a scaling factor which is related to the energy that’s contained in the signals that you are measuring the similarity.

For $Corr_{x,y}=0.95$ and $Corr_{y,z}=0.38$, $Corr$ ranges in $[-1, 1]$. Which can well score the similarity.

It’s worth noting that, sometimes, as seen in the code demo:

% This code highlights where non normalised correlation is
% be more beneficial than normalised correlation
t = [0:100-1]/100;
s1 = cos(2*pi*1*t);
s2 = cos(2*pi*4*t);
s3 = cos(2*pi*10*t);

% The following signals contain the three sinusoids above
a = 2*s1+4*s2+s3;
b = s1 + s2;

% Comparing the results it can be seen that non-normalised
% correlation is useful for identifying how strongly present
% one signal is in another
corr_res1 = sum(a.*s1)
norm_corr_res1 = sum(a.*s1)/sqrt((sum(a.^2).*sum(s1.^2)))

corr_res2 = sum(b.*s1)
nor_corr_res2 = sum(b.*s1)/sqrt((sum(b.^2).*sum(s1.^2)))

The output is:

>> NormalisedCorrelation

corr_res1 =

   100


   norm_corr_res1 =

       0.4364


       corr_res2 =

          50.0000


          nor_corr_res2 =

              0.7071