Define an Adjacency Matrix

Here, I want to define a matrix to show the graph or a network which has four nodes. As you can see in the Figure.
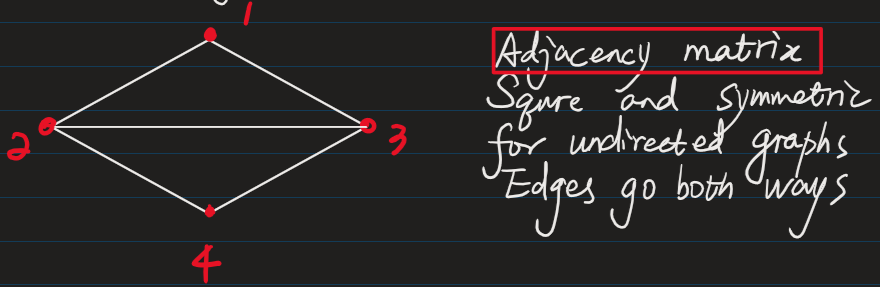
This is a 0-1 matrix with sij = 1 when nodes i and j are connectd by an edge. $$S_{ij} =
\begin{bmatrix} 0 & 1 & 1 & 0
1 & 0 & 1 & 1
1 & 1 & 1 & 0
0 & 1 & 1 & 0
\end{bmatrix} $$ This adjacency matrix means count the connection (edge) between node i and node j with one walk. For example, $S_{12}$ means from node 1 to node 2, there is one connection. And because there is no connection with one walk between node 1 itself, so $S_{11}$ equals to 0.
It’s a very excellent model for counting paths on a graph - channels of communication. And what we want to explore is how we can try to extend the function of this model? Look at at the $S_{ij}^2$: $$(S^2){ij} =
\begin{bmatrix} 2 & 1 & 1 & 2
1 & 3 & 2 & 1
1 & 2 & 3 & 1
2 & 1 & 1 & 2
\end{bmatrix} $$ We got a new model to represent something more interesting. To understand what it means, I wil show the expansion: $$(S^2){ij} = (row\,i\,of\,S)\cdot(column\,j\,of\,S) = s_{i1}s_{1j}+s_{i2}s_{2j}+s_{i3}s_{3j}+s_{i4}s_{4j} \tag{1}$$ We can get the conclusion, $(S^2)_{ij}$ means how many connections between node i and node j with a walk step of two. But why?
For better understanding this new model, we make the $(S^2)_{23}$ as an example as shown in the figure bellow. 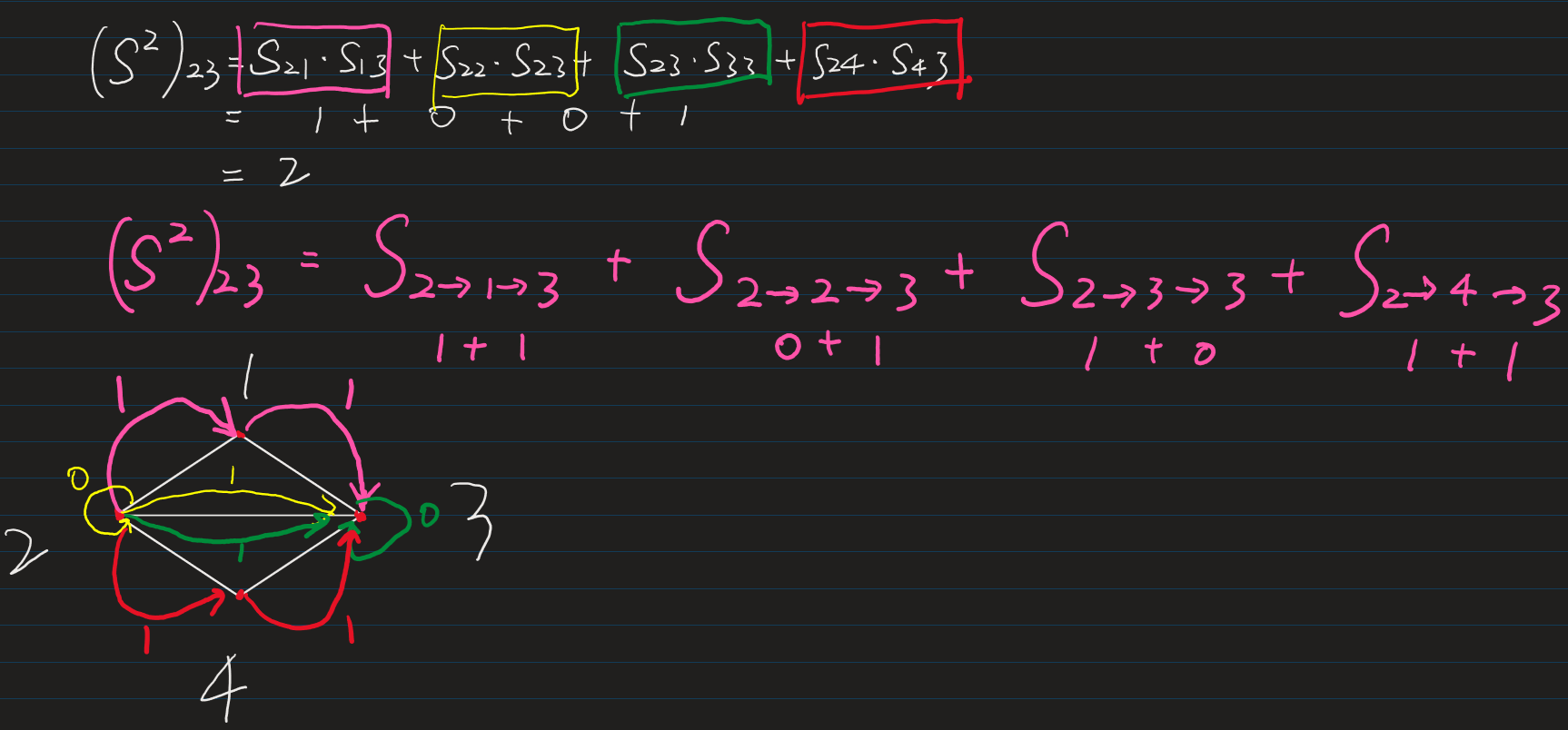$(S^2)_{23}$ has been expanded to 4 kind of walks, decomposed into $S_{21}\cdot S_{13} + S_{22}\cdot S_{23} + S_{23}\cdot S_{33} + S_{24}\cdot S_{43}$, make all this value into these terms from $S_{ij}$, and then we will find the value of this 4 steps. Only $S_{2\to 1\to 3}$ and $S_{2\to 4\to 3}$ equal to 2, so the value of $(S^2)_{23}$ equals to 2. Just the same with the result from (1).
The same, we can get $S^N$ counts all the N-step paths between pairs of nodes.